Como Calcular uma Treliça Metálica usando o Método dos Nós

Seja muito bem vindo a mais um exercício resolvido. Aqui quem fala é o Eng. Felipe Jacob e hoje vamos resolver passo a passo uma análise de treliça metálica plana utilizando o método dos nós.

Esse não é o único método possível para obter os esforços em treliças planas mas eu gosto dele por ser particularmente simples e exigir do estudante apenas conceitos básicos de trigonometria e noções sobre equilíbrios de forças.

Então, se você quer aprender como se calcula os esforços de uma treliça metálica plana usando esse método, ou se você quer relembrar como se faz isso, continue acompanhando até o fim.

Bibliografia Recomendada: BEER, Ferdinand P., JOHNSTON, E. Russel – Mecânica Vetorial para Engenheiros: Estática, 9ª Edição. McGrawHill.

Treliça Metálica a ser calculada pelo método dos nós

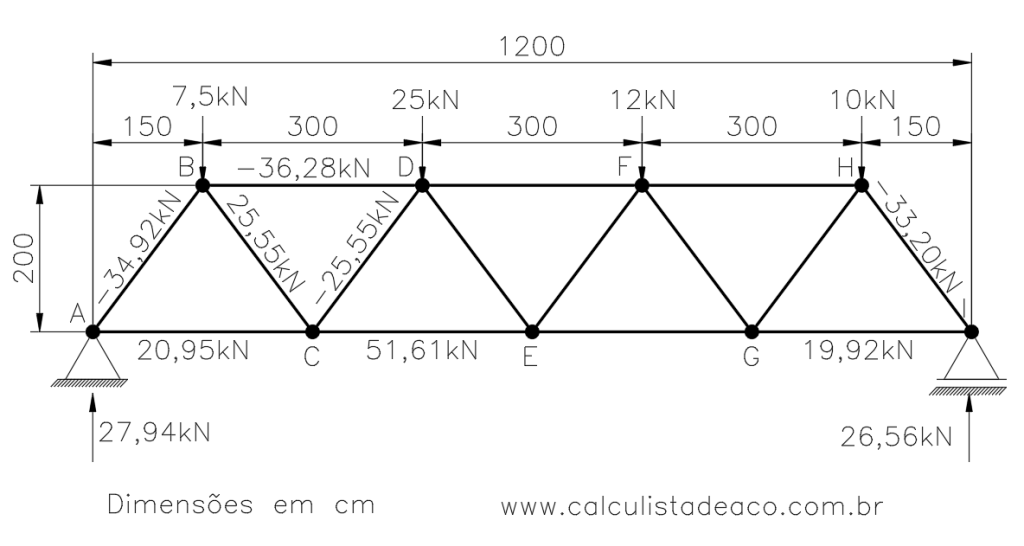
Nesse exercício resolvido de aplicação do método dos nós para análise de treliças planas vamos calcular uma treliça isostática de banzos paralelos, com uma concepção bastante usada em pontes e passarelas de pedestres.

O vão livre é de 12m (1200cm) e temos cargas pontuais diferentes aplicadas em cada um dos nós do banzo superior.

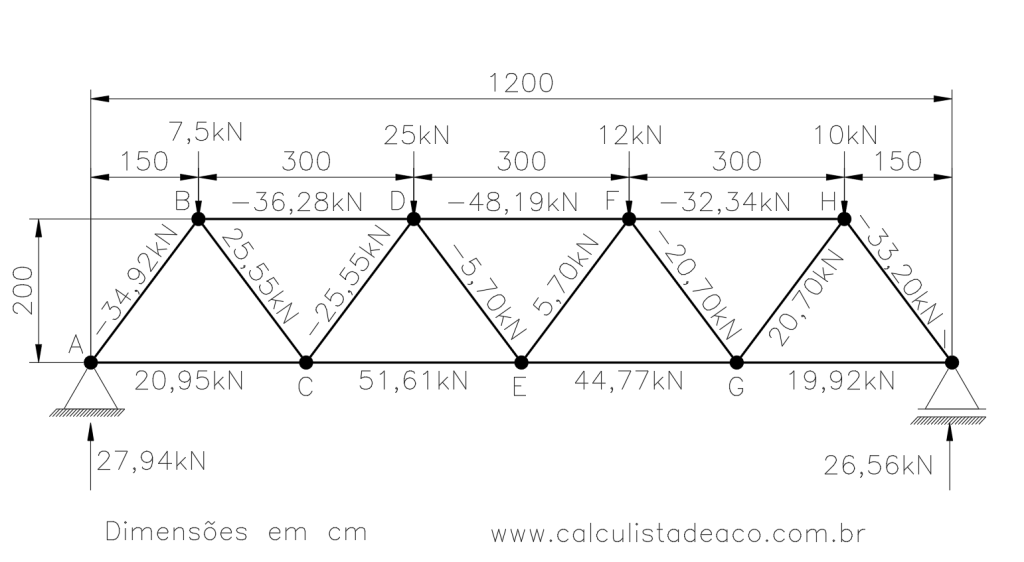
O objetivo desse exercício resolvido é calcular os esforços em todas as barras da treliça plana, determinar se são esforços de tração ou compressão e determinar as reações de apoio da estrutura.

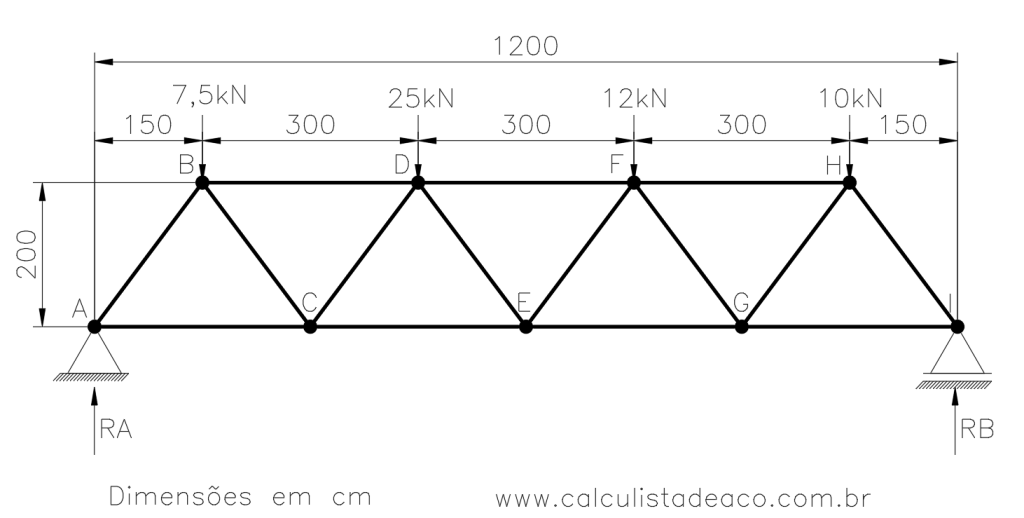
Passo 1: Determinar as reações de apoio da treliça plana

Para que haja equilíbrio da estrutura é necessário que três condições sejam satisfeitas:

A primeira delas é que a soma dos momentos seja igual zero, caso contrário a estrutura não estaria parada, mas sim girando.

Para satisfazer essa condição partimos de um ponto de apoio qualquer, escolhemos um sentido de giro como positivo e fazemos a soma dos momentos multiplicando as cargas aplicadas nos nós pela distância desse nó em relação ao ponto de apoio escolhido.

Escolhendo o ponto A para dar início, podemos escrever em notação matemática:

\sum{M_A} = 0

Considerando arbitrariamente o sentido horário como positivo, podemos escrever:

7,5. 150 + 25 . (450)+12 . (750) + 10 . (1050) - R_B . 1200 = 0

Podemos então calcular o valor de RB com facilidade

R_B= \frac{7,5. 150 + 25 . (450)+12 . (750) + 10 . (1050)}{1200}

R_B = 26,56 kN

A segunda condição a ser atendida é que a soma das cargas horizontais (x) e verticais (y) devem se igualar a zero, caso contrário a estrutura não estaria parada, mas se movimentando linearmente.

\sum{F_x} = 0

Como não há cargas horizontais aplicadas na treliça, não haverá reações horizontais nos pontos A e B.

Já para a direção vertical (y) é fácil deduzir que a reação RA somada com RB deve igualar-se às forças aplicadas no sentido vertical para baixo. Em linguagem matemática escrevemos:

R_A+ R_B = 7,5 +25 + 12 + 10

Já sabemos que o valor de RB é 26,56 kN, portanto podemos escrever:

R_A + 26,56 = 7,5 + 25 + 12 + 10

R_A= 7,5 + 25 + 12 + 10 - 26,56

R_A = 27,94 kN

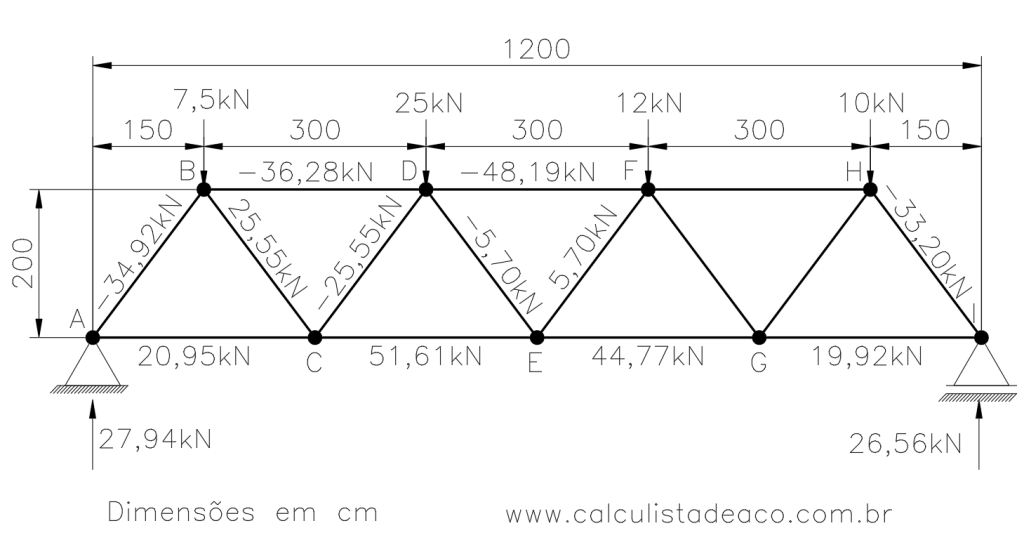
Assim conseguimos obter as reações de apoio em cada um dos nós e nosso diagrama ficou da seguinte forma:

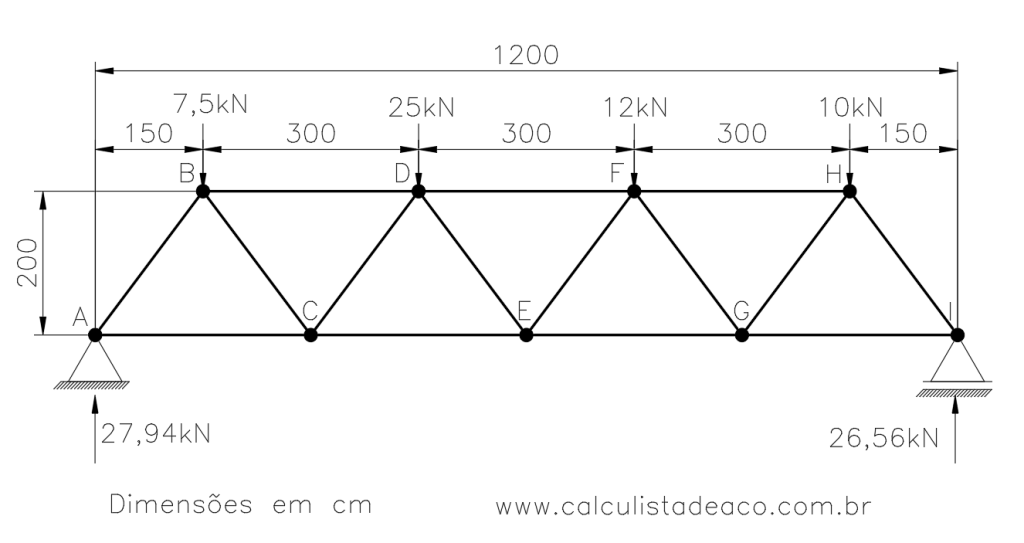
Agora que sabemos as reações de apoio, podemos iniciar nossos cálculos verificando as condições de equilíbrio vertical e horizontal de cada nó

Passo 2: Desenhar o diagrama de corpo livre de cada nó e aplicar as condições de equilíbrio de forças

Convenção de sinais: Vetor para a direita ou para baixo são considerados positivos. Vetores apontando para a esquerda ou para cima são considerados negativos. Forças saindo dos nós são positivas e indicam tração, forças entrando nos nós são negativas e indicam compressão

Vamos iniciar nossa análise à partir de um nó que esteja submetido a apenas duas forças incógnitas, ou que apresente somente duas barras saindo dele. Podemos iniciar pelo nó A ou pelo nó I. Por comodidade vamos iniciar pelo nó A.

Representaremos as forças incógnitas inicialmente sempre saindo dos nós, e se após o cálculo o valor obtido for positivo, indica que acertamos sua orientação e a barra está tracionada. Se o valor obtido for negativo indica que devemos mudar a orientação da força apontando-a para o nó e o valor indica compressão

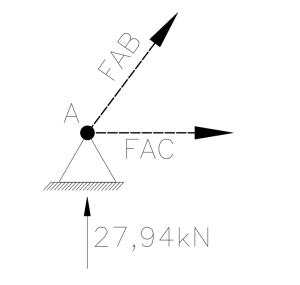
Na imagem acima temos um detalhe das forças atuantes no nó A. Na direção vertical temos a reação de apoio de 27,94 kN obtida anteriormente, enquanto as barras AB e AC apresentarão forças FAB e FAC respectivamente.

Dessa forma os esforços FAB e FAC podem ser obtidos por cálculos trigonométricos simples.

Poderíamos fazer isso de várias formas diferentes, mas vamos partir do que eu acredito ser mais simples: obtendo o seno e cosseno do ângulo θ, conseguimos obter os valores de FAB e FAC por semelhança de triângulos. Para isso, vamos primeiro calcular o comprimento da barra AB por um simples teorema de Pitágoras

L_{AB} = \sqrt{200² + 150²}

L_{AB} = 250cm

De posse do comprimento da Barra AB podemos então calcular calcular o esforço nessa barra (FAB) fazendo o equilíbrio das forças verticais

\sum F_{y} = 0 \rightarrow 27,94 + F_{AB} . \frac{200}{250} = 0

F_{AB}  = \frac{-27,92}{0,8}

F_{AB} = -34,92 kN

Logo, a barra AB apresenta compressão (por causa do sinal negativo) com valor de 34,92 kN.

A força na barra AC pode ser obtida fazendo-se o equilíbrio de forças na horizontal:

\sum F_{x} = 0 \rightarrow F_{AC} + (-34,92) . \frac{150}{250} = 0

F_{AC} = 34,92 . 0,8

F_{AC} = 20,95 kN

Como o vetor FAC sai do nó A (ver figura 3), a barra AC possui esforço positivo de tração igual a 20,95 kN

Dessa forma já conseguimos determinar os esforços nas barras AB e AC, e nossa treliça então fica dessa forma:

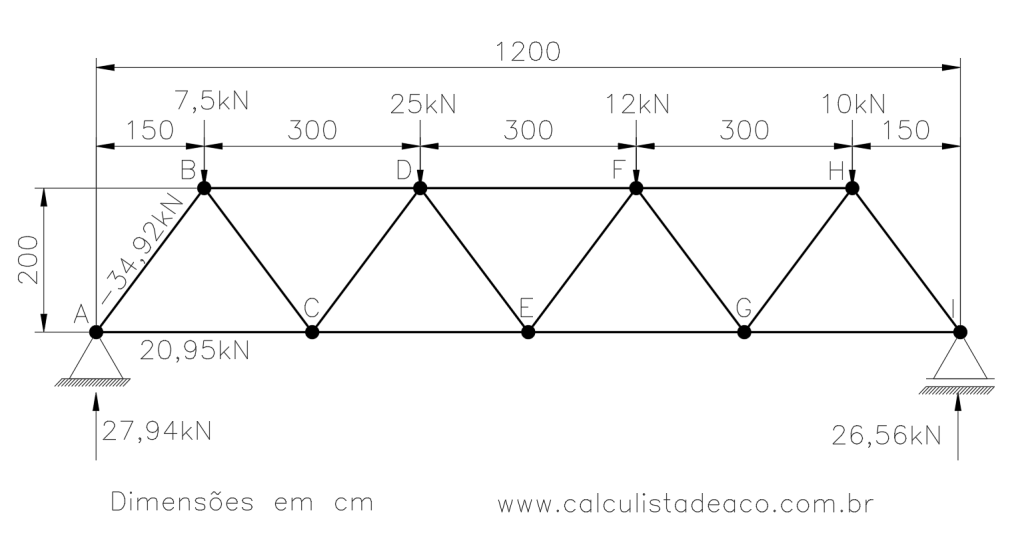
Vamos aproveitar o embalo e fazer o mesmo procedimento no nó I, já que temos praticamente as mesmas condições.

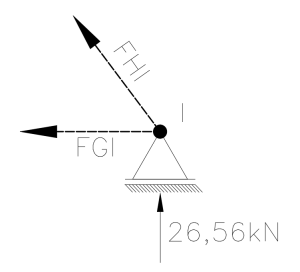
Como a treliça é simétrica, as dimensões do lado direito são as mesmas do lado esquerdo, portanto podemos proceder exatamente da mesma maneira:

\sum F_{y} = 0 \rightarrow 26,56 + F_{HI} . \frac{200}{250} = 0

F_{HI} = -33,20 kN

Com a força de compressão obtida na barra HI, podemos deduzir a força na barra GI:

-F_{GI} + 33,20.\frac{150}{250} = 0

F_{GI} = 19,92 kN

Assim temos mais um trecho da nossa treliça com os esforços devidamente calculados:

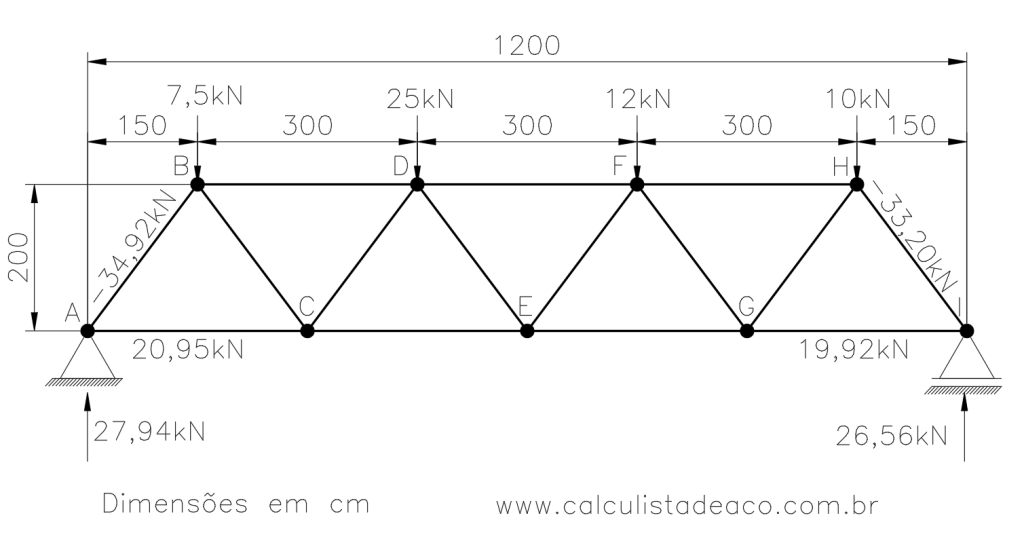
Agora podemos avançar para o nó B ou para o nó H. Vamos escolher o Nó B por conveniência.

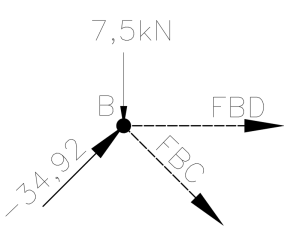
Primeiro vamos analisar as forças horizontais. As forças FAB (-34,92 kN) e FBC estão inclinadas em relação à força FBD. Portanto as componentes horizontais de FAB e FBC somadas com a força FBD devem igualar-se a zero para que haja equilíbrio na direção horizontal. Assumindo vetores para a direita como positivos e para a esquerda como negativos, temos:

\sum{F_x}=0 \Rightarrow 34,92 . \frac{150}{250} + F_{BC} . \frac{150}{250} + F_{BD} = 0

Simplificando temos:

20,95 + 0,6 . F_{BC} + F_{BD} = 0

Como ainda não é possível determinar nem o valor de FBC nem FBD, precisamos analisar o equilíbrio das forças verticais. Temos uma carga vertical externa de 7,5 kN atuando no nó B, e as componentes verticais de FAB e FBC. Todas essas cargas devem anular-se, somando zero para haver o equilíbrio de forças no nó Assumindo vetor apontando para cima como negativo e para baixo como positivo, podemos escrever:

\sum{F_y}=0 \Rightarrow -34,92 . \frac{200}{250} + F_{BC} . \frac{200}{250} + 7,5 = 0

Agora temos uma equação com apenas uma incógnita e podemos determinar o valor de FBC com facilidade:

F_{BC} = \frac{-7,5 +34,92 . 0,8}{0,8}

F_{BC} = 25,55 kN

Como o sinal deu positivo, mantemos a direção do vetor indicando que esta barra está tracionada.

Agora podemos voltar na equação de equilíbrio horizontal e substituir FBC:

20,95 + 0,6 . F_{BC} + F_{BD} = 0

20,95 + 0,6 . 25,55 + F_{BD} = 0

F_{BD} = - 36,28 kN

Como encontramos sinal negativo, indica que essa barra está comprimida e o vetor chega no nó B.

Assim temos mais um trecho da nossa treliça com os esforços devidamente calculados:

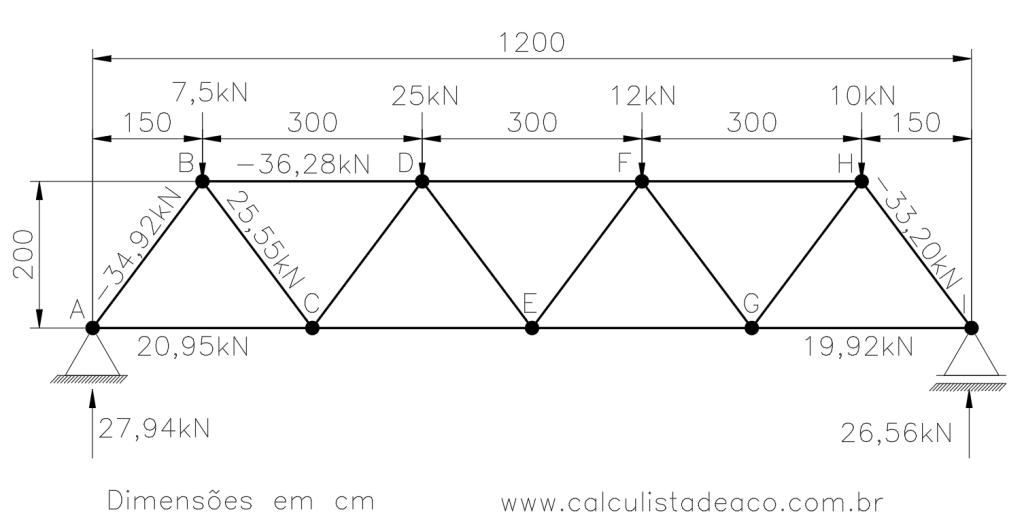
Já deu pra perceber que o macete é sempre partir para um nó com apenas duas forças incógnitas. Poderíamos avançar para o nó C para determinar as forças FCD e FCE, ou então analisar o nó H para encontrar as forças FHG e FFH.

Seguimos para o nó C.

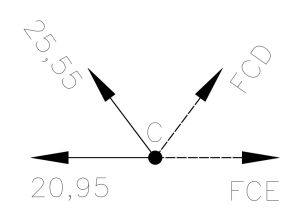
no nó C temos duas forças com módulo, direção e sentido já conhecidas (FAC e FBC), e duas forças incógnitas (FCD e FCE)

Novamente vamos calcular as condições de equilíbrio horizontal e vertical

Para o equilíbrio vertical, as componentes verticais de FCD e FBC somadas devem anular-se. mantendo a mesma convenção de sinais (direita = positivo, para baixo = positivo) temos:

\sum{F_y}=0 \Rightarrow -25,55 . \frac{200}{250} - F_{CD} . \frac{200}{250} = 0

F_{CD} = -25,55 kN

Portanto o valor da força na barra CD tem mesmo módulo que o valor na barra BC, porém em sentido oposto, sendo comprimida ao invés de tracionada.

Analisando agora no sentido horizontal, podemos escrever:

\sum{F_x}=0 \Rightarrow -20,95 -25,55 . \frac{150}{250} + F_{CE}  + F_{CD} . \frac{150}{250} = 0

Substituindo FCD encontrado há pouco escrevemos:

\sum{F_x}=0 \Rightarrow -20,95 -25,55 . \frac{150}{250} + F_{CE}  + (-25,55) . \frac{150}{250} = 0

Podemos então encontrar FCE:

F_{CE} = 20,95 + 25,55 . 0,6 + 25,55 . 0,6 \Rightarrow F_{CE} = 51,61 kN

com sinal positivo indicando tração. Assim mais duas barras de nossa treliça tiveram seus esforços determinados.

Já que estamos nesse embalo vamos para o nó D, que apresenta apenas duas forças incógnitas.

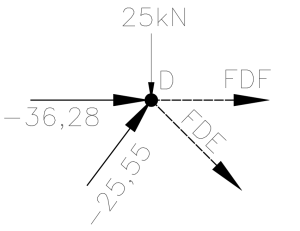
Não tem novidade alguma aqui, vamos seguir com os procedimentos que fizemos para todos os nós anteriores

\sum{F_y}=0 \Rightarrow -25,55 . \frac{200}{250} + F_{DE} . \frac{200}{250} + 25 = 0

F_{DE} = -5,70 kN

Essa foi bem fácil… agora na horizontal:

\sum{F_x}=0 \Rightarrow 36,28 + 25,55 . \frac{150}{250} + F_{DE} . \frac{150}{250} + F_{DF}  +  = 0

Substituindo FDE encontrado anteriormente temos

\sum{F_x}=0 \Rightarrow 36,28 + 25,55 . \frac{150}{250} + (-5,70) . \frac{150}{250} + F_{DF}  +  = 0

F_{DF}= 5,70 . 0,6 - 25,55 . 0,6 - 36,28 \Rightarrow F_{DF} = -48,19 kN

Mais duas forças incógnitas foram desvendadas, deixando nossa treliça assim:

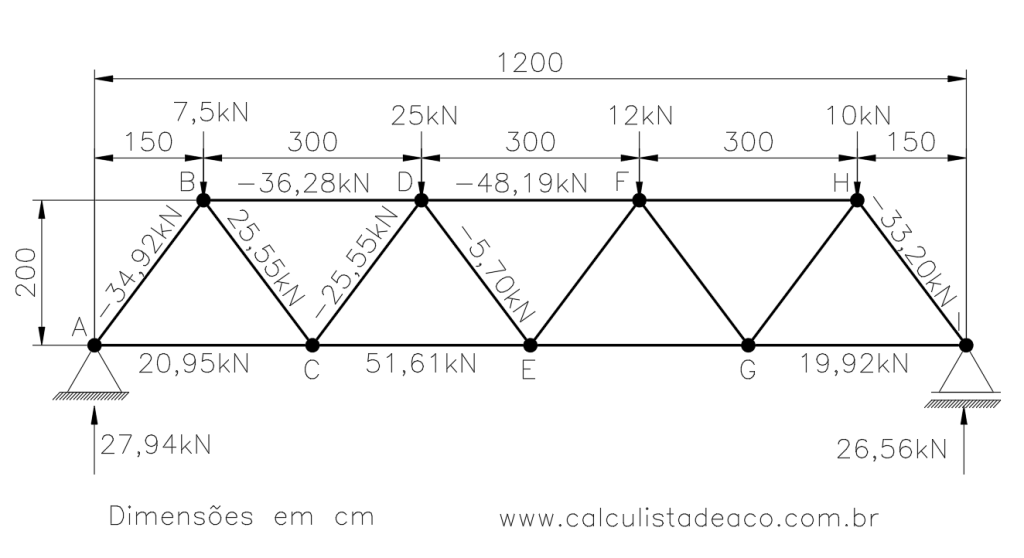
Seguimos nossa marcha de cálculo, agora rumo ao nó E:

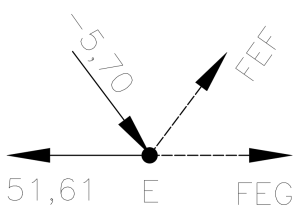
É tudo repetição do que já foi dito, não desanimem, já passamos da metade!

\sum{F_y}=0 \Rightarrow -5,70 . \frac{200}{250} + F_{EF} . \frac{200}{250} = 0

F_{EF} = 5,70 kN

Mais uma barra tracionada, e vamos para o equilíbrio de forças na horizontal:

\sum{F_x}=0 \Rightarrow -51,61 + 5,70 . \frac{150}{250} + F_{EF} . \frac{150}{250} + F_{EG}  = 0

\sum{F_x}=0 \Rightarrow -51,61 + 5,70 . \frac{150}{250} + 5,70 . \frac{150}{250} + F_{EG}  = 0

F_{EG}= 44,77 kN

E assim temos mais duas forças desmascaradas:

Agora será possível resolver qualquer um dos nós que restaram, já que todos eles apresentam no máximo. vamos analisar o nó G:

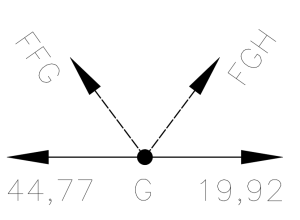
e lá vamos nós de novo…. aguenta aí que está acabando…

\sum{F_y}=0 \Rightarrow -F_{FG} . \frac{200}{250} - F_{GH} . \frac{200}{250} = 0

\sum{F_y}=0 \Rightarrow -F_{FG} . 0,8- F_{GH} . 0,8 = 0

F_{FG}  = - F_{GH}

Não foi possível determinar o valor de nenhuma das forças nas FG ou GH, somente que ambas tem sinais opostos, vamos ver se e equilíbrio na direção horizontal nos darão mais sorte:

\sum{F_x}=0 \Rightarrow -44,77- F_{FG} . \frac{150}{250} + F_{GH} . \frac{150}{250} + 19,92 = 0

F_{GH} . 0,6 - F_{FG} . 0,6 = - 19,92 + 44,77

Porém como sabemos de FFG = – FGH podemos substituir FGH na equação:

F_{GH} . 0,6 - (-F_{GH} . 0,6) = 24,85

2 . F_{GH}.0,6 = 24,85

F_{GH} = 20,70 kN

Logo:

F_{FG} = -20,70 kN

E assim estamos quase terminando de determinar os esforços na nossa treliça, falta apenas uma barra!

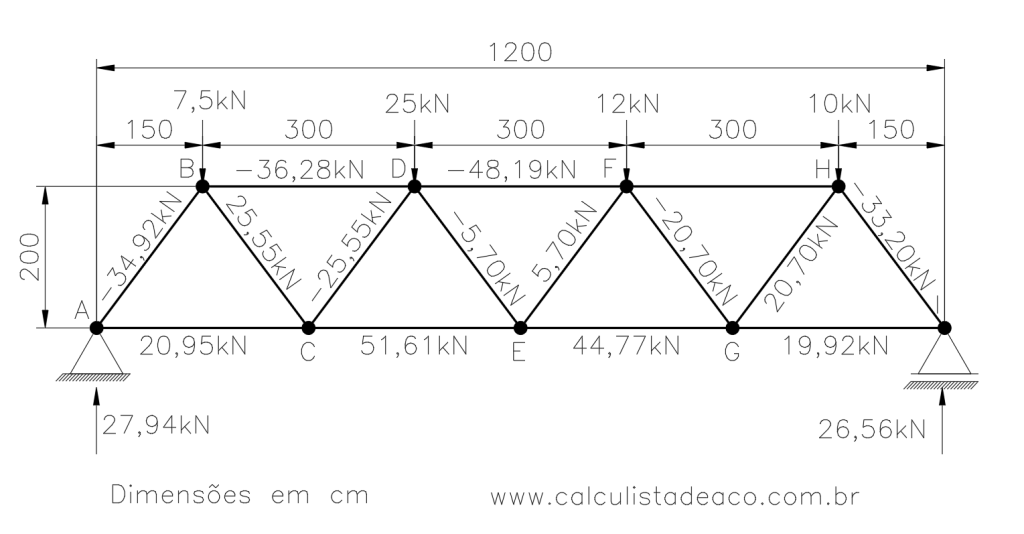
Podemos encontrar os esforços na barra FH partindo tanto do nó F como do nó H. Por pura comodidade, vamos calcular à partir do nó H por ter apenas 3 barras e uma força, enquanto no nó F teríamos que lidar com 4 barras e uma força.

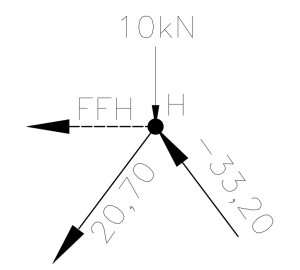
Lembrando que consideramos para baixo e para a direita como positivos, e para cima e à esquerda negativos.

Como não temos nenhuma força incógnita na vertical, vamos partir do equilíbrio horizontal de forças:

\sum{F_x}=0 \Rightarrow -F_{FH} - 20,70 . \frac{150}{250} - 33,20 . \frac{150}{250} = 0

F_{FH} =  -20,70 . 0,6 - 33,20 . 0,6

F_{FH} =  -32,34 kN

E assim conseguimos finalizar o cálculo completo os esforços na treliça plana:

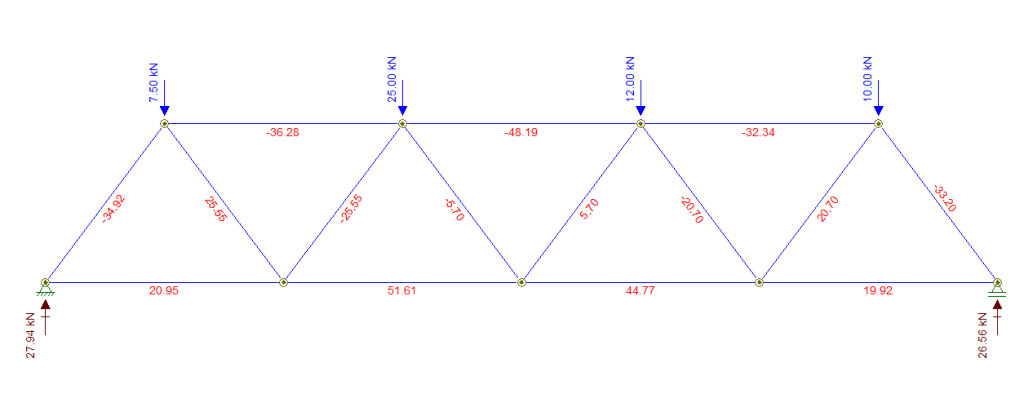
Para conferir os resultados podemos comparar com os resultados obtidos no ftool por exemplo:

E assim concluímos um exercício resolvido passo a passo. Espero que tenha gostado, se gostou, compartilhe esse conteúdo com alguém que possa gostar!

Grande abraço e até a próxima!

Eng. Felipe Jacob