Como Calcular Zx e Zy – Módulo Resistente Plástico de Perfis em Estruturas Metálicas
Seja muito bem vindo ao blog do Calculista de Aço, aqui quem fala é o Eng Felipe Jacob e nesse artigo vou demonstrar como você pode calcular o módulo plástico Zx e Zy de qualquer perfil metálico usando o Autocad como ferramenta.
Eu também expliquei tudo em forma de vídeo, e se preferir pode ver ele aqui abaixo:
O que é e para que serve o Módulo Resistente Plástico Zx e Zy?
Caso você já conheça a teoria por trás dessa propriedade geométrica e só quer saber como calcular usando o Autocad, pode pular essa parte e ir direto para o passo 1. Mas caso queira compreender para saber aplicá-la de forma consciente, continue lendo a explicação abaixo.
Trata-se de uma das propriedades geométricas das seções transversais que são necessárias para dimensionar peças submetidas à flexão, de acordo com a norma NBR8800/08.
A resistência última teórica de um barra submetida a momento fletor se dá pelo Momento de Plastificação, ou Mpl:
Eq. 1: \space \space \space \space \space \space \space \space \space \space \space Mpl = Z.F_y
Ou seja, o Momento fletor que leva a peça à plastificação total da seção, portanto, à formação do fenômeno da Rótula Plástica, é igual ao Módulo Resistente Plástico multiplicado pelo limite de escoamento do material.
Eu sei, o que eu falei acima não ajuda muita coisa… então vamos partir para uma explicação mais detalhada para que você possa compreender o fenômeno físico que essa propriedade traduz.
Considere uma barra qualquer, submetida à flexão: surgem tensões de tração e compressão acima e abaixo da linha neutra, da seguinte forma:
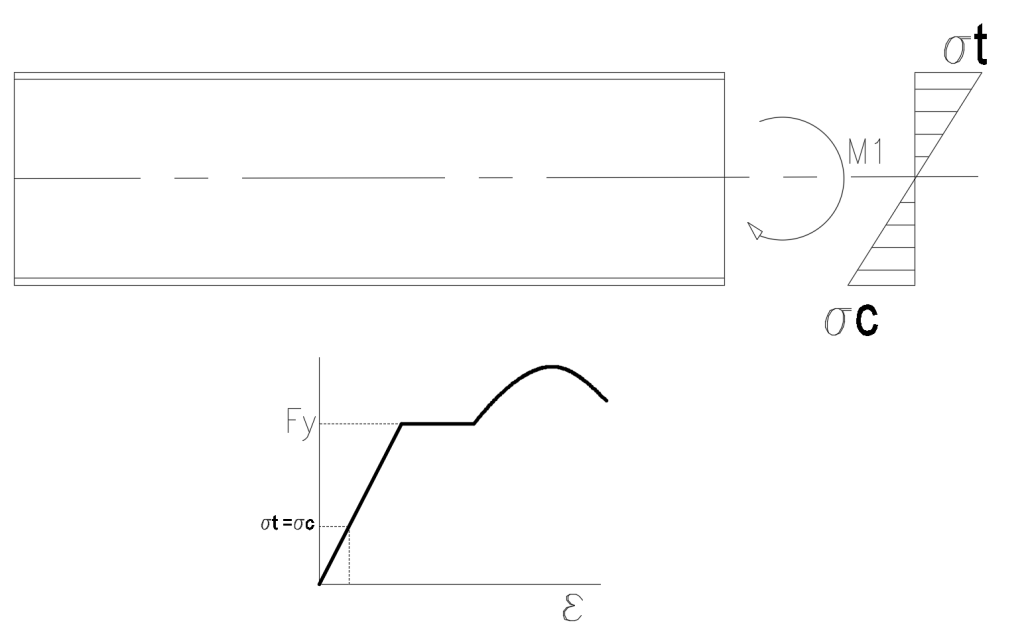
Na figura 1 vemos uma peça submetida ao Momento Fletor M1, que produz as tensões de compressão σ-c e de tração σ-t
Observe no gráfico logo abaixo da viga que a tensão aplicada é inferior à tensão limite de escoamento Fy. Isso significa que a peça está em regime elástico, ou seja, se o momento fletor for removido, a peça voltará ao estado de deformação inicial, justamente como uma mola ideal. Este é o estado desejado para qualquer peça que se deseja usar para fins estruturais.
Nessas condições, para saber qual é a tensão atuante, basta aplicar a seguinte equação:
Eq. 2: \space \space \space \space \space \space \space \space \space \space \spaceσ_c = σ_t = {M_1.y \above{1pt} I}Sendo:
M1 = Momento fletor aplicado na barra
y = distância da linha neutra da peça até o ponto em que se deseja obter a tensão. Caso queira a máxima tensão, basta considerar y como a distância da linha neutra até a extremidade da peça.
I = Momento de Inércia da seção transversal da barra em questão.
Se continuarmos a aumentar o momento fletor M aplicado, até que as tensões atuantes atinjam o limite de escoamento do material, mas não ultrapasse esse limite, teremos a seguinte configuração:
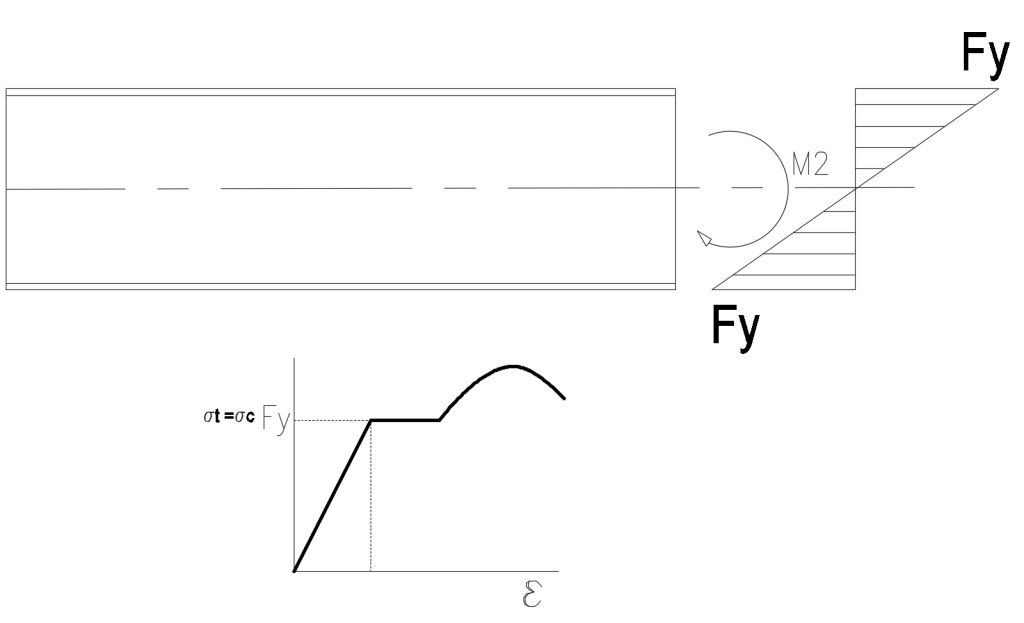
Na condição acima, temos o maior momento fletor ao qual a peça pode ser submetida antes de ultrapassar os limite de escoamento Fy da barra. Podemos, portanto, chamar a esse estágio Limite Elástico, pois a barra ainda está se comportando como uma mola ideal, porém, qualquer acréscimo de Momento Fletor ocasionará o início do comportamento plástico da peça com deformações permanentes.
Para descrever matematicamente este estágio, assumindo que nos interessa apenas a máxima tensão, ou seja, a que ocorre quando y é a distância da linha neutra ao topo (ou base) da peça, basta trocar os σ por Fy já que a tensão atuante nesse ponto será idêntica ao limite de escoamento:
Eq. 3: \space \space \space \space \space \space \space \space \space \space \space F_y= {M_2.y \above{1pt} I}Porém, já existe uma constante que define a Inércia dividido pela distância da linha neutra à extremidade: é o módulo resistente elástico, ou W da peça. Sabendo que W = I/y quando y é igual à distância da linha neutra à extremidade da peça, e reorganizando a Eq.3 para descrevê-la em função do momento fletor, que no momento é o que nos interessa, teremos:
Eq. 4: \space \space \space \space \space \space \space \space \space \space \space M_2= {W.F_y }Se você já andou folheando antigos livros de resistência dos materiais, ou já teve contato com a antiga norma de estruturas de aço, a NB-14, que trabalhava na filosofia do Método das Tensões Admissíveis, certamente já deve ter visto a Eq. 4 ou alguma variação dela com fatores de segurança aplicados. Essa era a forma que se definia o maior momento fletor ao qual a peça poderia estar submetida antes de ultrapassar o regime elástico, e por isso essa metodologia é chamada de análise plástica do material.
Porém, desde a versão de 1988, a norma brasileira NBR8800 passou a adotar a análise plástica como metodologia para avaliar barras prismáticas de seção constante submetidas ao momento fletor e por isso, passou a ser necessário usar outra propriedade geométrica que não o W para determinar qual seria o maior momento fletor ao qual a peça poderia estar submetida, e assim determinar os limites de projeto adequados para a nova forma de calcular. Essa propriedade é o Z e a partir de agora ela vai entrar em ação.
Continuemos com nossa explicação;
Sabemos que até o presente momento, nossa peça está submetida a um momento fletor que, apesar de ser o maior momento ao qual a peça pode ser submetida antes de plastificar, ele ainda não tira a peça do comportamento elástico. Portanto, se esse momento fletor for removido da peça, ela voltará então ao estágio inicial, sem qualquer deformação residual ou permanente.
Porém se continuarmos a aumentar esse momento fletor, observaremos que as partes mais extremas da peça não terão a tensão aumentada, justamente por que naquela região o material já perdeu sua elasticidade ideal e começara a se comportar de maneira mais similar a uma massa de modelar do que como uma mola ideal.
A figura abaixo ilustra isso de forma mais clara:
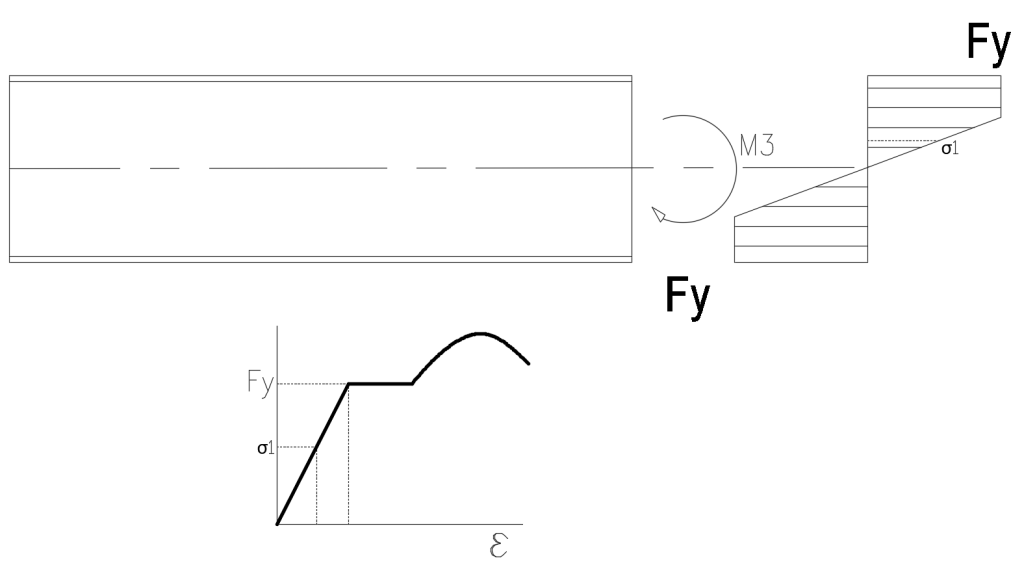
Quando a peça está no estágio descrito na figura 3, já ocorreu uma plastificação parcial da seção transversal, ou seja a região mais próxima das extremidades já atingiu o limite de escoamento e já não se comporta mais como uma mola, mas como uma massa de modelar. Por isso dizemos que essa região está em regime plástico. Porém, algumas partes da seção transversal ainda conservam o comportamento elástico, como é o caso da região onde temos a tensão σ1. Essa parte da peça ainda conserva alguma rigidez e comportamento elástico, e portanto dizemos que a plastificação foi parcial.
Porém, se aumentarmos ainda mais o momento fletor, finalmente chegaremos então ao estágio da Plastificação Total da Seção Transversal, que pode ser ilustrada conforme a seguir:
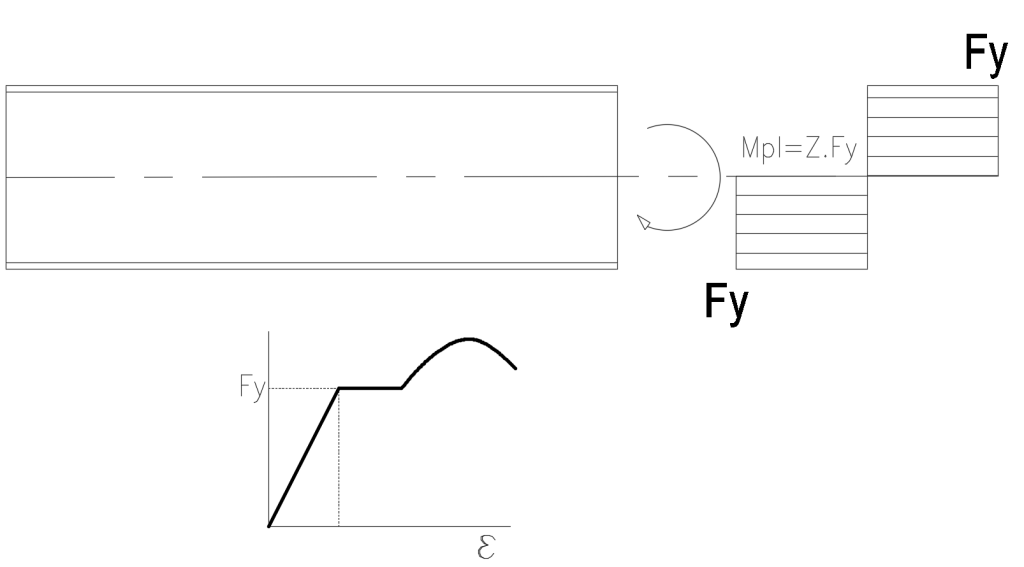
O estado de tensões acima ilustrado indica que a peça sofreu Plastificação Total em toda a sua seção transversal, ou seja, não há mais nenhuma parte que se comporte de forma elástica, mas 100% da peça se comportará como uma massa de modelar, sendo portanto o último estágio de resistência da barra flexionada.
No ponto em que essa plastificação ocorrer, surgirá o que chamamos de Rótula Plástica: por não haver mais rigidez elástica, aquele ponto se torna uma articulação e a estrutura vai ao colapso.
Para determinar matematicamente o momento fletor em que ocorre esse fenômeno, voltamos então para nossa Equação 1:
Eq. 1: \space \space \space \space \space \space \space \space \space \space \space Mpl = Z.F_y
Como o Z se trata de uma propriedade geométrica que está relacionada com a flexão, da mesma forma que o W, é usual representar essa propriedade através de um fator de forma que representa a relação entre Z e W.
Algumas literaturas técnicas como o Formulas for Stress and Strain trarão, por exemplo a notação SF = 1,25. Isso significa que o valor de Z é 1,25 x W.
No caso acima, SF vem de Shape Factor, que significa literalmente “Fator de Forma” cujo valor é Z/W.
Outras literaturas representam o fator de forma com a letra “k”. Mas o significado é o mesmo
Para encontrar o valor de Z basta multiplicar metade da área da seção transversal pela distância entre os dois eixos baricêntricos das seções transversais acima e abaixo da linha neutra do perfil:
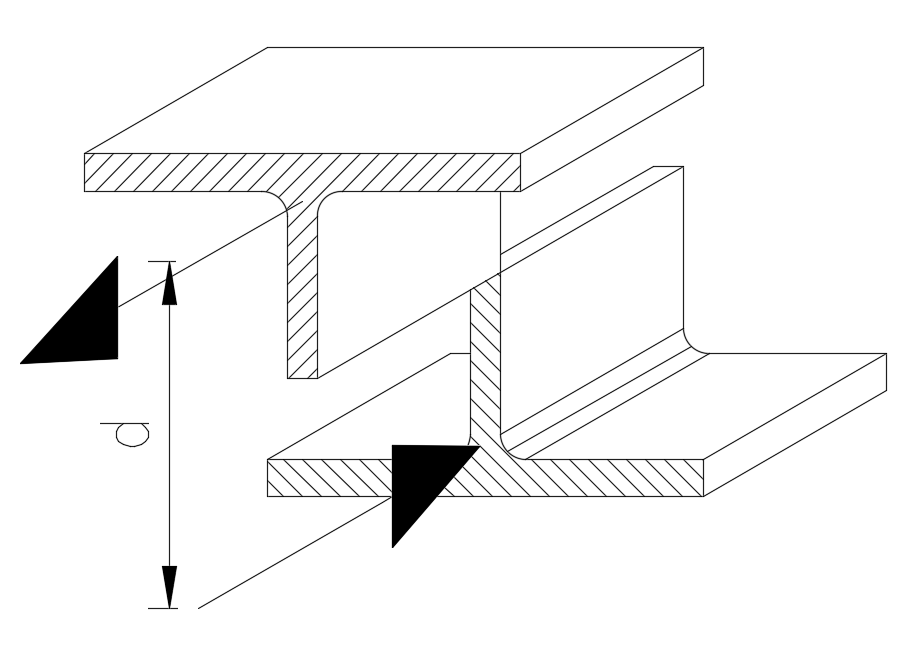
Na figura acima fica ilustrado que a parte superior da peça, sofrendo por exemplo tração, possui uma força resultante equivalente que pode ser representada como uma força pontual saindo do CG do “T” superior, enquanto o mesmo ocorre com a parte inferior da peça, porém na forma de compressão.
A formulação matemática para determinar o Z é simples:
Eq. 5: \space \space \space \space \space \space \space \space \space \space \space Z = {A. d \above{1pt} 2}Basta portanto multiplicar a área da seção transversal pela distância “d” entre os eixos baricêntricos e dividir por dois. Nosso trabalho então passa a ser uma tarefa de mecânica dos sólidos, e só precisamos encontrar esses centros baricêntricos. Podemos fazer isso através de métodos analíticos e manuais ou usando ferramentas como o autocad por exemplo. Aqui vamos explicar usando o Autocad.
Encontrando o Zx e Zy de Peças Simétricas
Passo 1: Desenhe a seção transversal desejada no autocad
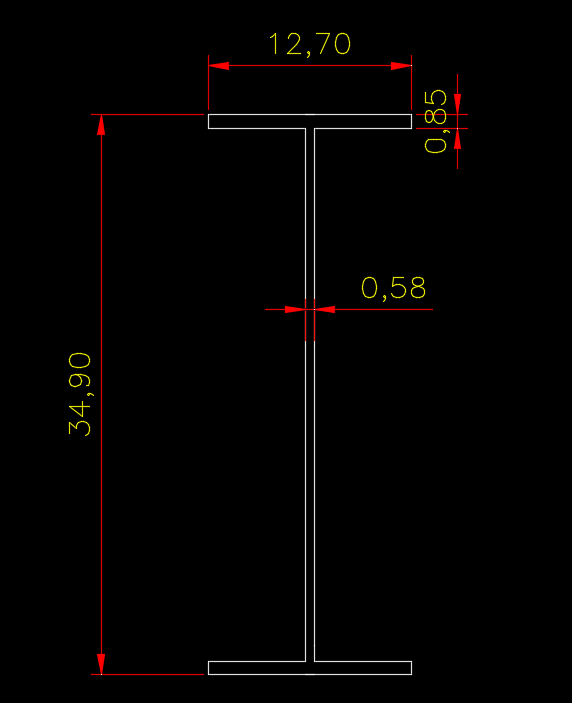
Primeiro você deve desenhar a seção transversal desejada no ambiente MODEL do seu Autocad. Para o nosso exemplo vamos trabalhar em um perfil I de abas paralelas, equivalente ao perfil W360X32,9 porém sem os raios de curvatura para termos a possibilidade de comparar os resultados com os apresentados pela tabela de bitolas Gerdau. Eu recomendo que façamos o desenho usando as dimensões em cm, para facilitar os cálculos posteriormente.
Passo 2: Obtenha as propriedades da seção com os comandos “Region” e “Massprop”
Digite o comando “Region”, selecione a seção transversal inteira. Na barra de comandos deve aparecer uma mensagem dizendo “1 region created” ou indicando mais regiões criadas caso a seção seja composta por mais figuras planas.
Antes de usar o comando Massprop você deve posicionar o seu eixo de origem em algum lugar próximo à peça, para posteriormente colocarmos no eixo baricêntrico da mesma. Para fazer isso digite o comando “UCS” e posicione a origem em algum lugar da peça, da seguinte forma:

Após posicionar a origem em um ponto qualquer, precisamos obter as coordenadas para colocar ela na posição do CG da peça, para isso digite o comando “Massprop” para obter as propriedades de massa atuais da seção.
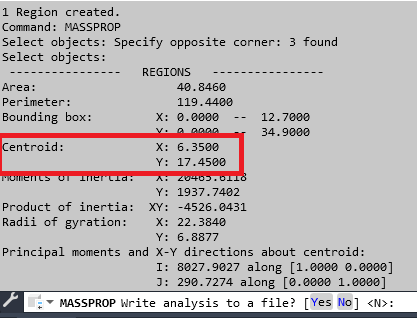
Passo3: divida a peça em duas partes acima e abaixo do centróide.
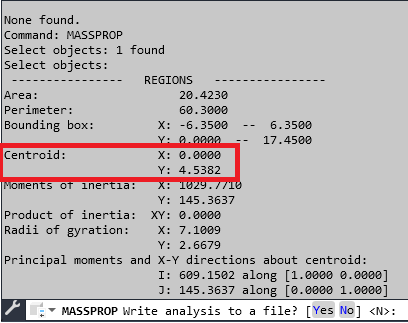
Observe que o comando massprop nos gerou um relatório que contém a área da seção transversal (40,846cm²), e também onde podemos saber a real posição do centroide em relação ao eixo UCS que determinamos. Vamos nesse primeiro exemplo mostrar como encontrar o Módulo Resistente Plástico em relação ao eixo X-X, portanto, vamos dividir a peça em duas partes, na altura de 17,45, e posicionar o UCS em um local de fácil acesso:
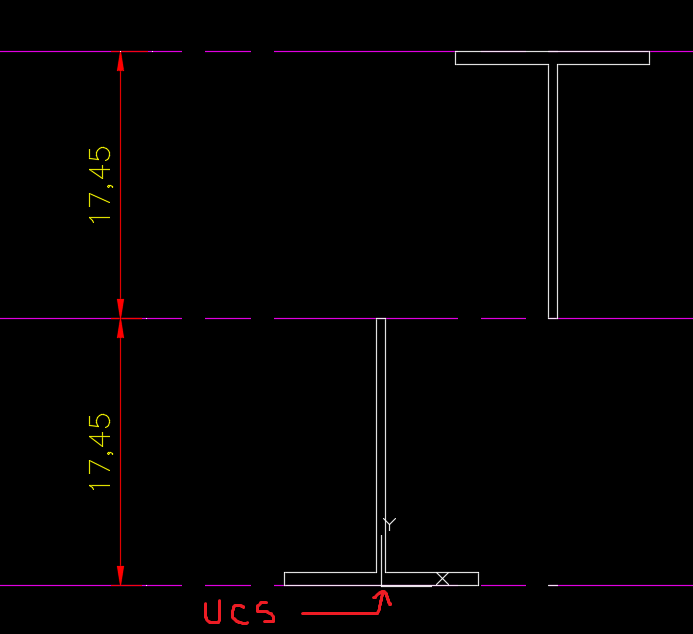
Passo 4: Encontre a posição do centróide de ambas partes separadas.
Agora devemos fazer o mesmo processo para cada uma das peças: Criar as regiões com “Region”, e usar o comando “Massprop” para cada parte individualmente, para finalmente encontrar o centroide de cada uma. Após isso basta traçar uma linha horizontal em cada centroide e medir a distância entre eles:
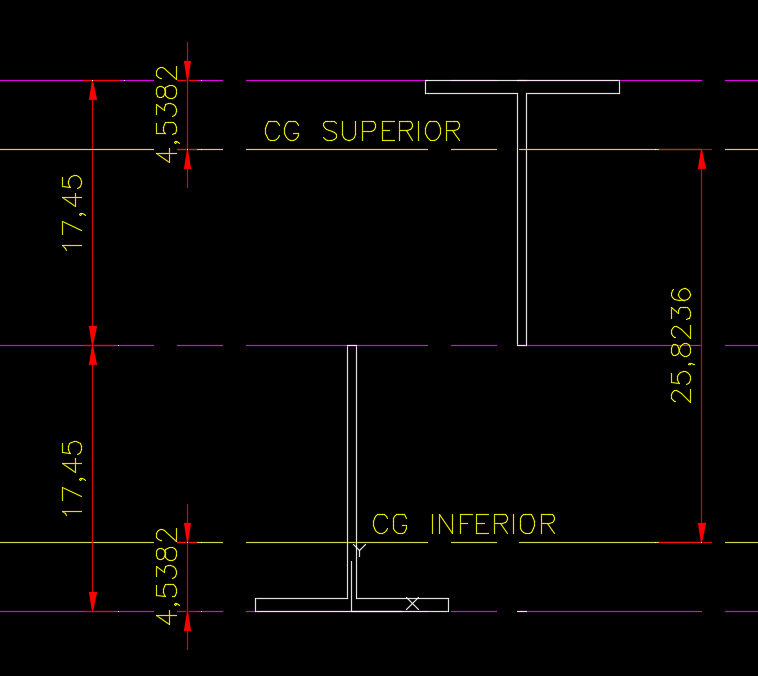
Passo 5: Aplique a fórmula
Agora basta aplicar a equação 5, com as informações obtidas: Área da seção (4,561 cm²) obtida no passo 2 e agora a distância entre os centróides (2,84cm)
Eq. 5: \space \space \space \space \space \space \space \space \space \space \space Z_x = {A. d \above{1pt} 2}Z_x = {40,486 \space . \space 25,8236 \above{1pt} 2}Z_x = \underline{527,3953 cm³}Ao consultar uma Tabela de Bitolas Gerdau, você vai perceber que o perfil W360X32,9 apresenta Zx = 547,6. Isso se dá devido à presença dos raios de curvatura que solidarizam a mesa à alma do perfil. Para efeitos práticos, essa pequena diferença não criará impacto significativo nos cálculos e está a favor da segurança
Concluímos dessa forma o cálculo da propriedade geométrica Zx para uma cantoneira de abas iguais
Caso você deseje obter o Zy, basta repetir o mesmo processo, porém dividindo a peça em duas partes a partir de uma linha vertical.
o mesmo procedimento pode ser realizado para qualquer seção transversal com simetria em relação ao eixo que se pretende calcular o Z. Porém esse processo não será o mesmo para seções assimétricas, que é o caso que veremos logo abaixo.
Encontrando os módulos resistentes plásticos Zx e Zy de Perfis Assimétricos
Quando calculamos as propriedades de uma seção transversal simétrica em relação ao eixo baricêntrico, como é o caso do perfil I que calculamos acima, a Posição da Linha Neutra Elástica coincide com a posição da Linha Neutra Plástica, sendo portanto bem fácil saber exatamente o ponto onde devemos fazer a divisão da peça em duas partes.
Porém, no caso de uma seção assimétrica, há um distanciamento entre as duas linhas neutras.
A Linha Neutra Elástica está posicionada de tal forma que a soma dos momentos estáticos de ambos lados seja zero. Porém a Linha Neutra Plástica se localiza numa posição que divide a peça em duas figuras geométricas com áreas iguais, uma acima e outra abaixo dela mesma.
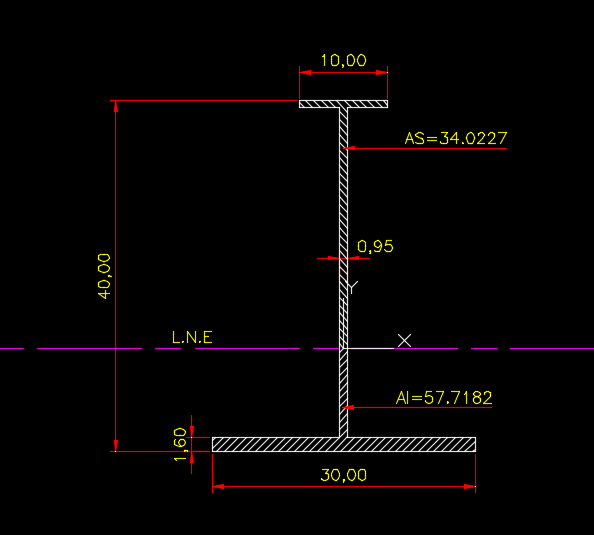
Na figura 12 foi feito o processo de obtenção do centroide (Linha Neutra Elástica) para um perfil assimétrico, e podemos observar que as duas figuras formadas, inferior e superior não possuem áreas idênticas, e por isso a Linha Neutra Plástica deve estar em outro lugar.
Como não sabemos inicialmente se a Linha Neutra Plástica corta a alma do perfil ou se está localizada cruzando a mesa do mesmo, vamos ter que iniciar partindo de uma dessas hipóteses e se os cálculos forem inconsistentes, devemos tentar de outra maneira.
Vamos partir da hipótese inicial de que a L.N.P passa pela alma do perfil a uma altura y acima da face superior da mesa inferior, conforme fig. 12.
Eq. 6: \space \space \space \space \space \space \space \space \space \space \space A_s = A_i \to \space B_s.t_s + (d`-y).t_w = B_i.t_i + y.t_w
A equação acima diz que devemos igualar As (área superior) com Ai (Área inferior). Para isso vamos igualar a área da mesa superior (Bs x ts) somada à cota que vai da face inferior da mesa superior até a Linha Neutra Plástica, multiplicado pela espessura da alma, com os mesmos elementos da parte inferior.
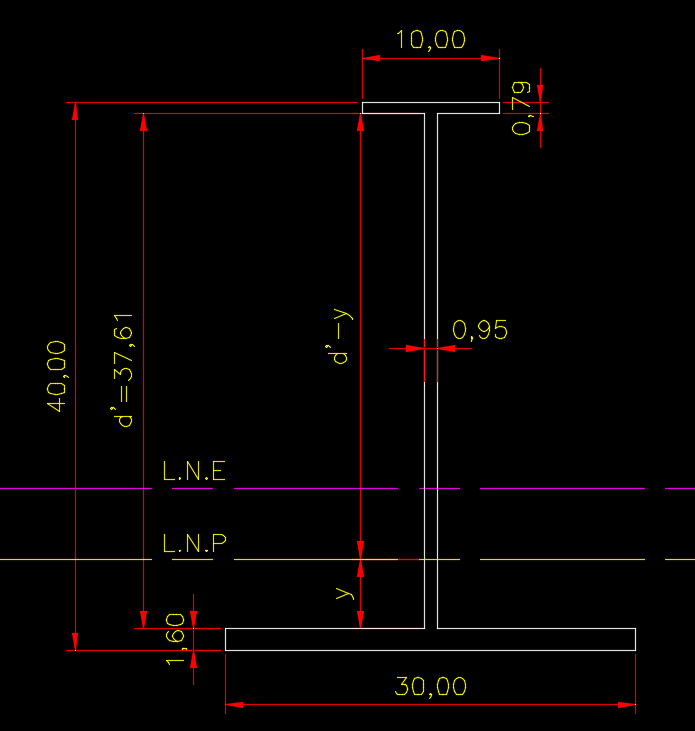
Resolvendo a equação 6 com as medidas da figura 12 temos
Eq. 6: \space \space \space \space \space \space \space \space \space \space \space A_s = A_i \to \space B_s.t_s + (d`-y).t_w = B_i.t_i + y.t_w
Eq. 6: \space \space \space \space \space \space \space \space \space \space \space 10 \space.\space 0,79 + (37.61-y)\space.\space0,952 = 30 \space . \space 1.60+ 0,952\space.\space y = -2.25
Observe que ao aplicar a equação 6 obtivemos um valor negativo, e isso significa que erramos na nossa hipótese e nossa Linha Neutra Plástica cruzará não a alma do perfil mas sim a mesa inferior, conforme fig. 13. Sendo assim temos que mudar a estratégia de cálculo, elaborando uma equação que melhor represente essa nova condição:
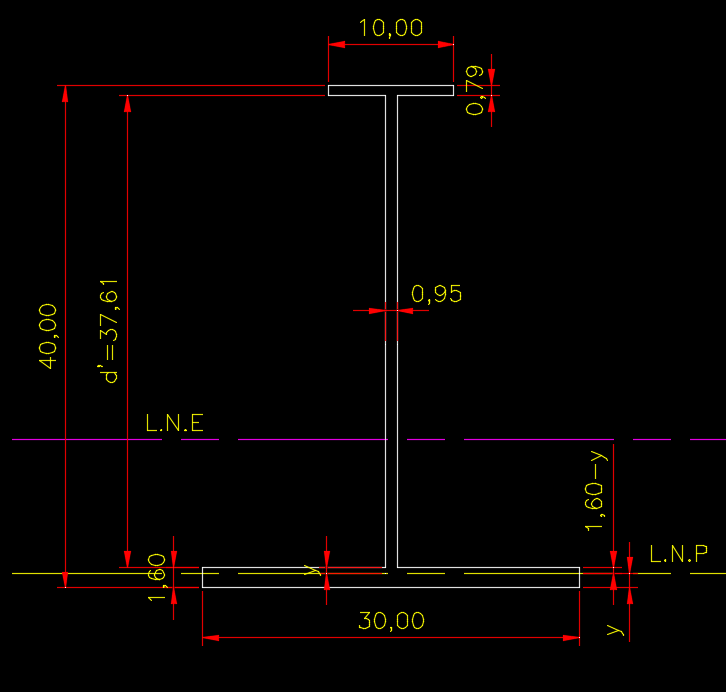
Nesse caso faremos o cálculo de acordo com a equação 7
Eq. 7: \space \space \space \space \space \space \space \space \space \space \space A_s = A_i \to \space B_s.t_s + d`.t_w + B_i.(t_i-y) = B_i.y
Eq. 7: \space \space \space \space \space \space \space \space \space \space \space 10 . 0,79 + 37,61 . 0,952 + 30.(1,60-y) = 30.y
y = 1,52833cm
Vamos posicionar portanto a Linha Neutra Plástica a 1,52833cm acima da base do perfil, criar uma hachura para cada parte da peça e comparar as duas áreas:
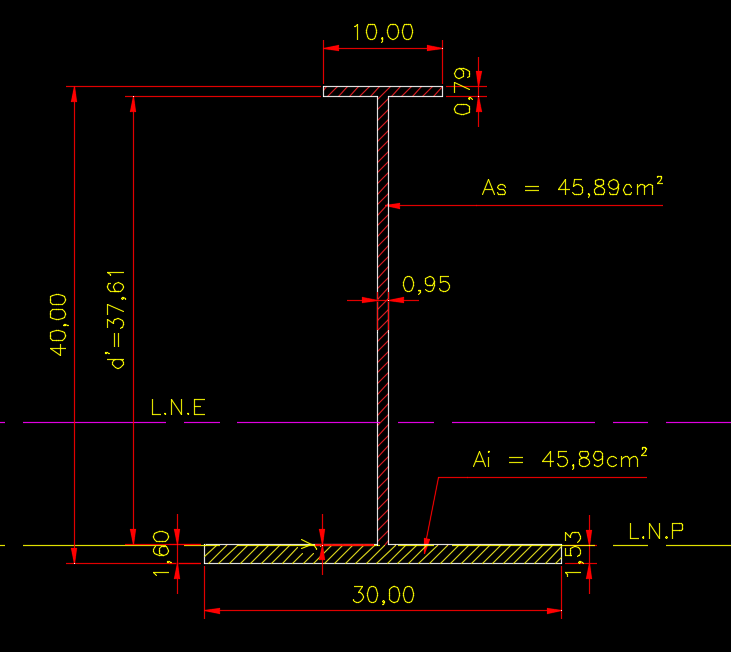
Agora que já sabemos a posição da Linha Neutra Plástica, devemos seguir obtendo os respectivos baricentros de ambas figuras que se formaram, e aplicar a equação 5 para finalizar o cálculo
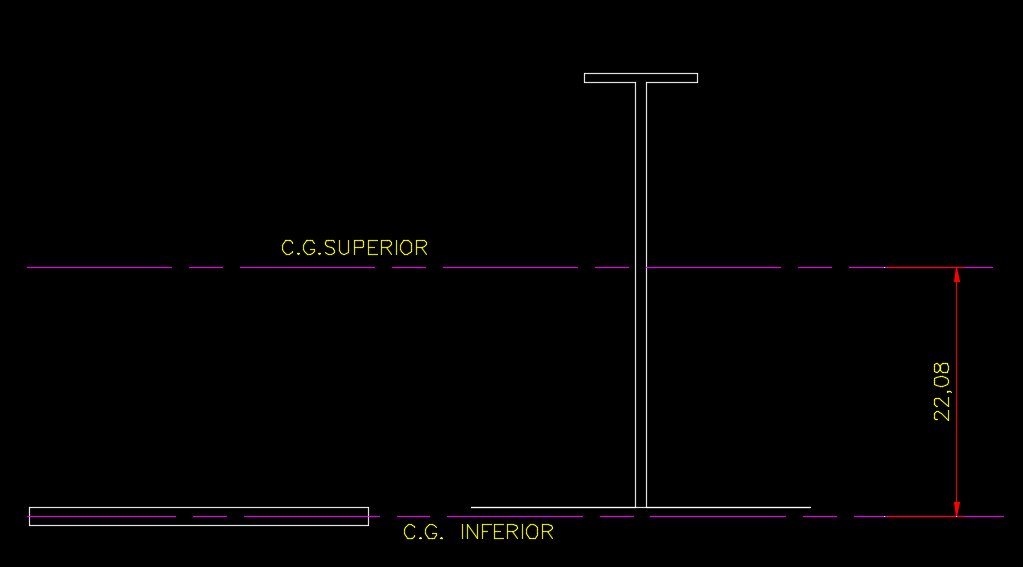
Aplicando na equação 5:
Eq. 5: \space \space \space \space \space \space \space \space \space \space \space Z_x = {A. d \above{1pt} 2}Z_x = {(2.45,89). 22,08 \above{1pt} 2}Z_x = 1013,25 cm³
E assim finalizamos o cálculo de Zx para um perfil assimétrico.
Espero que tenha gostado desse conteúdo, se tem alguma dúvida pode postar nos comentários.
Aproveito para deixar um agradecimento especial ao prof. Cereno Muniz que colaborou com a produção desse artigo. http://linkedin.com/in/cereno-muniz-76880430
Grande abraço e até a próxima
Eng. Felipe Jacob
Muito legal Felipe, continue nos ensinando, sou seguidor de suas newsletters que são de fácil compreenção e demostram seu alto nivel de conhecimento, com uma facilidade comunicação. Parabéns