Como obter as reações de apoio de estruturas metálicas apoiadas sobre colunas de concreto armado?

Bibliografia Recomendada: BEER, Ferdinand P., JOHNSTON, E. Russel – Mecânica Vetorial para Engenheiros: Estática, 9ª Edição. McGrawHill.

Olá, seja muito bem vindo mais uma vez ao meu blog, Eng Felipe Jacob aqui e nesse artigo quero ajudar você a resolver um dos problemas que mais tiram o sono dos calculistas na hora de elaborar projetos de estruturas metálicas para coberturas: Como obter as as reações de apoio de estruturas metálicas repousadas sobre colunas de concreto armado da forma correta.

Para explicar esse tema, vou usar como exemplo um caso muito comum que geralmente só é percebido quando o calculista da estrutura metálica passa as reações de apoio no topo das colunas de concreto para o calculista de concreto armado, e este percebe que as cargas estão absurdamente altas, gerando colunas de dimensões aparentemente exageradas.

Instaura-se então a discórdia: o calculista da estrutura metálica jura de pés juntos que passou as cargas certas e o calculista de concreto armado diz que aquelas cargas são absurdas e que tem algo errado com o cálculo da estrutura metálica.

Quem está certo nesse caso? Não vou fazer mistério, nesse exemplo acima, o calculista do concreto armado geralmente tem razão e a causa é um erro de avaliação por parte do calculista de estruturas metálicas, e para evitar esse tipo de problema é necessário primeiro entender as suas causas.

Não confunda topo de pilar com apoio rígido

O problema acima é causado principalmente por uma confusão no uso de apoios de primeiro, segundo ou terceiro gêneros por parte dos calculistas de estruturas metálicas.

Vamos começar nossa explicação investigando como se comportam esses diferentes tipos de apoio adotados nos cálculos de estruturas metálicas para coberturas, e qual a forma correta de abordar esse assunto.

Para auxiliar no entendimento modelei no ftool uma treliça metálica com vão livre de 20m e cargas unitárias nos nós, com o intuito apenas de investigar as reações de apoio obtidas à partir das diferentes abordagens possíveis.

O caso mais comum de se ver (e também o que mais causa problemas) é a adoção de apoios de segundo gênero fixos para ambos lados da estrutura, como no exemplo abaixo:

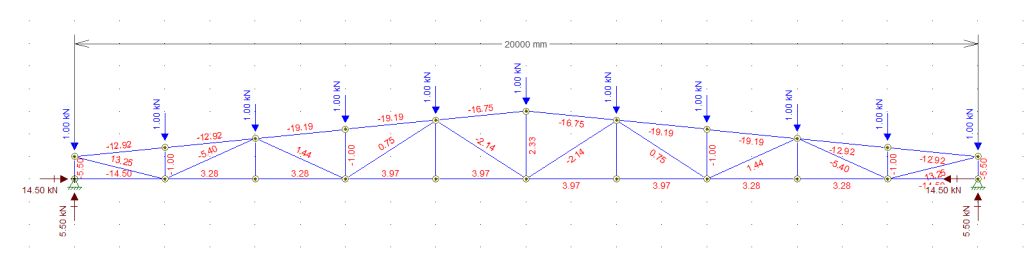
Com essa configuração obtivemos uma “reação” no apoio com valor de 14,50 kN. Se você observar com mais atenção, vai perceber que o trecho central do banzo inferior, parte que está mais distante dos apoios apresenta um esforço de tração, com valor 3,97 kN enquanto os trechos mais próximos dos apoios apresentam um valor elevado de compressão, idêntico à reação do próprio apoio, ou seja, 14,50 kN.

Isso acontece pelo fato de a estrutura ser hiperestática e a rigidez do apoio e das barras influenciam diretamente nos valores dessas reações de apoio no topo de colunas de concreto. Mas para simplificar essa explicação usando uma frase mais simples, poderíamos dizer que “rigidez atrai esforços”, ou seja, quanto mais rígido for o apoio e quanto mais rígidas forem as barras que compõem a estrutura, maior será o valor dessa reação horizontal.

Agora vamos ver o que acontece quando removemos toda a rigidez horizontal dos apoios da treliça, adotando um apoio de primeiro gênero com liberdade de translação na horizontal:

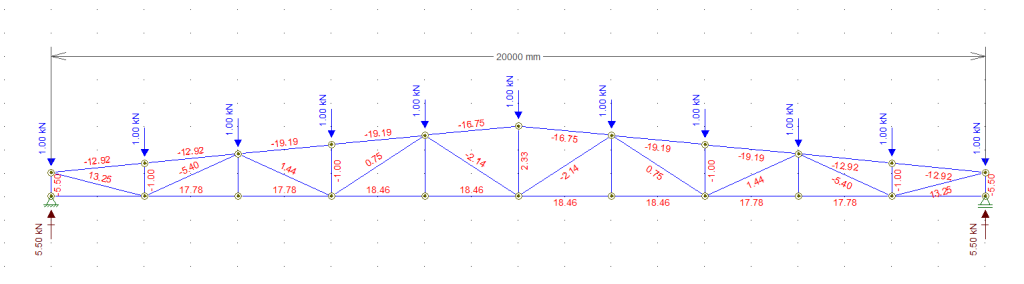
As reações de apoio horizontais simplesmente desaparecem e ficamos apenas com as reações de apoio verticais que devem ser obrigatoriamente a soma das cargas impostas à estrutura. No banzo inferior restou apenas tração com um valor de 18,46 kN no centro e zero nas extremidades.
Lembra do que eu disse: “Rigidez atrai esforços”? Sem qualquer rigidez horizontal nos apoios, as reações nessa direção também vão a zero.

E se fizermos um terceiro teste, oferecendo ao apoio um apoio nem tão rígido, nem totalmente livre na horizontal?

para isso adotamos um apoio com coeficiente de mola, conforme abaixo:

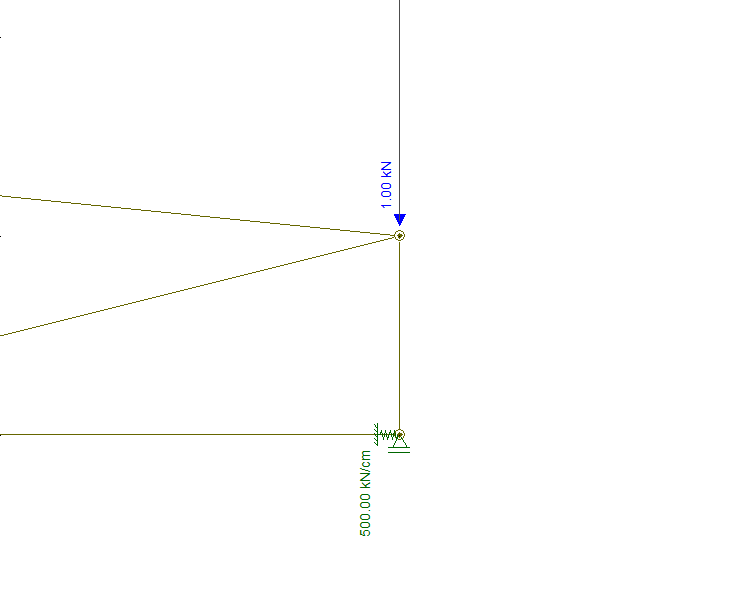
O apoio acima foi adotado apenas no lado direito da treliça, e indica que ele possui uma rigidez limitada na direção X.

Mas o que significa adotar um coeficiente de mola para apoios sobre coluna de concreto?

Lembra da lei de Hooke?

F = K. \Delta x

Traduzindo: a força aplicada numa mola é diretamente proporcional à deformação Δx multiplicado pelo coeficiente de rigidez K dessa mola.

Podemos então reescrever:

K = \frac {F} {\Delta x}

Assim podemos ler: a rigidez da mola é a força aplicada dividido pela deformação resultante.

Em termos ainda mais simples: O valor de 500 kN/cm é o K do apoio, e se ele fosse uma mola (e de fato é) seria necessário uma força de 500 kN para que ele se deslocasse 1cm horizontalmente.

Assim sendo, após rodar o cálculo temos o seguinte resultado:

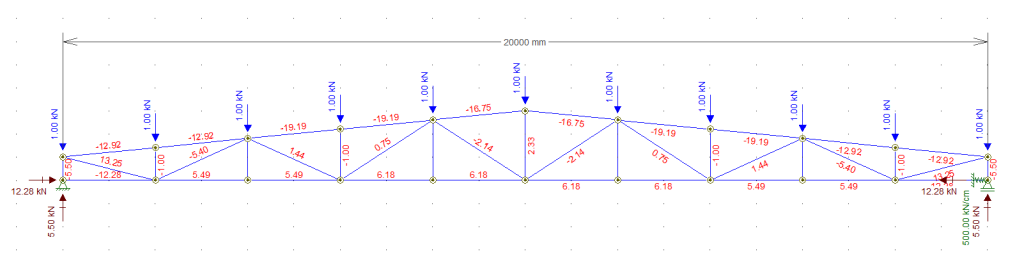
Obtivemos uma reação de apoio horizontal de 12,28 kN. Ora, não é o mesmo valor que obtivemos no primeiro teste (14,50 kN) mas também não é zero. Isso significa que obtivemos uma reação de apoio intermediária pois usamos uma rigidez limitada para aquele ponto específico.

Vamos reduzir a rigidez pela metade para ver o que acontece:

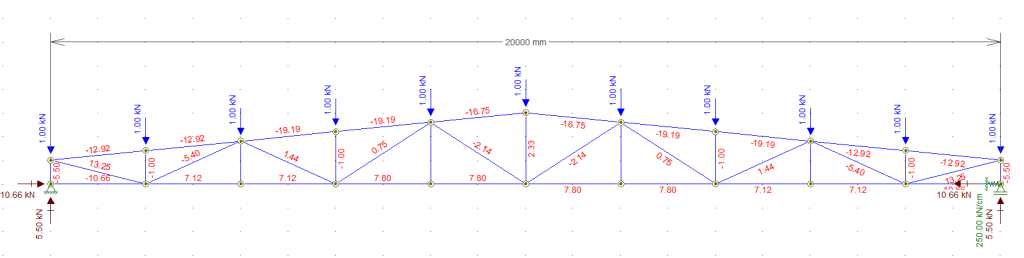
após reduzir a rigidez K do apoio para 250 kN/cm, a reação de apoio baixou para 10,66 kN.
Interessante, não é mesmo?

E se baixarmos a rigidez pela metade novamente, o que será que acontece?

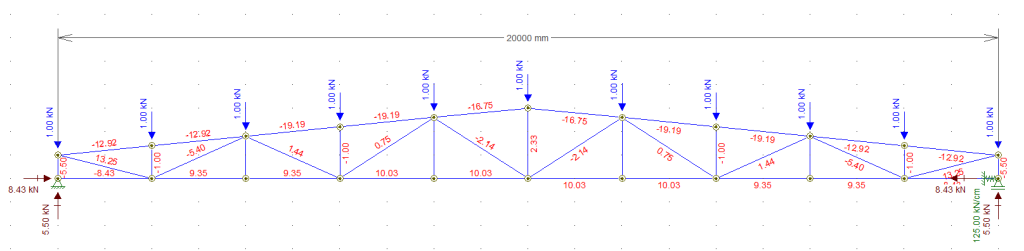
Baixamos a reação de apoio para 8,43 kN usando uma rigidez e 125 kN/cm. Comprovamos assim que há uma relação direta entre a reação de apoio e a rigidez do mesmo apoio.

Motivado por nada mais que pura curiosidade, me entreguei ao trabalho de plotar um gráfico para ver como seria a forma da curva que essa relação teria, e ficou assim:

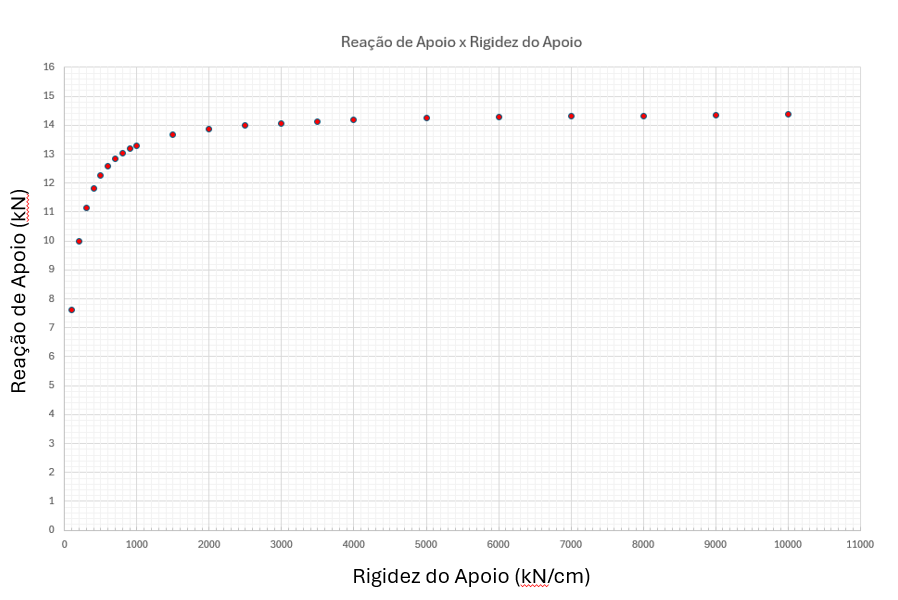
O gráfico acima nos mostra que a reação de apoio não aumenta na mesma proporção que a rigidez aplicada, mas apresenta uma curva assintótica, ou seja, que tende ao valor máximo (14,50 kN) mas que nunca de fato atinge esse valor.

Podemos também observar que, para esse caso específico, há uma grande diferença nas reações obtidas dentro do intervalo entre 0 e 2000 kN/cm, mas acima dessa rigidez a diferença é muito pequena, quase desprezível.

Ou seja, dependendo da rigidez do topo da nossa coluna, podemos obter um erro muito grande nas reações de apoio e causar um superdimensionamento das colunas de concreto, além de mascarar esforços importantes na nossa treliça, uma vez que a rigidez nos apoios influencia diretamente o valor das cargas de compressão e tração atuantes nos banzos da treliça metálica.

Como contabilizar a rigidez correta do topo das colunas de concreto armado

Como falamos anteriormente, a rigidez de um ponto qualquer é a razão entre a força aplicada e sua deformação:

K = \frac {F} {\Delta x}

Considerando que colunas geralmente são barras engastadas na extremidade inferior e livres na extremidade superior, podemos assumir o seguinte esquema:

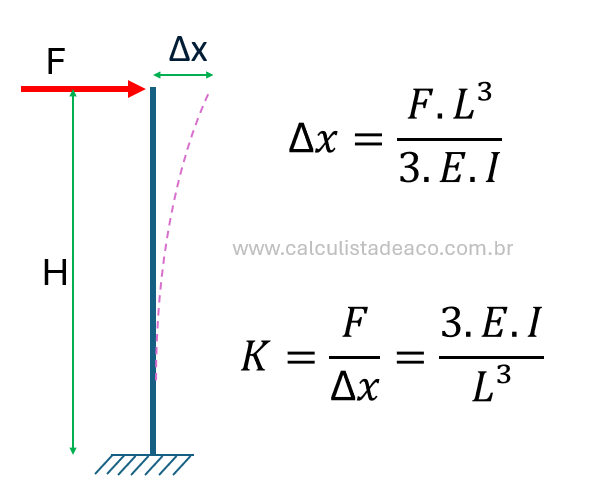
De forma mais específica considerando uma coluna de formato quadrado ou retangular, podemos substituir o momento de inércia na equação do K que fica:

K = \frac {3 . E . B. A³} { L³ . 12} 

Que simplificando resulta em:

K = \frac {E_{cs} . B. A³} { 4L³} 

Sendo A a dimensão da coluna no plano da treliça (altura da seção) e B a dimensão da coluna perpendicular à treliça (largura da seção). O Ecs é o módulo de elasticidade secante do concreto em kN/cm² que pode ser calculado pela equação:

E_{cs}=0,085 . 5600 . \sqrt{f_{ck}}

Exemplo:

Suponha que a treliça de 20m do exemplo anterior esteja apoiada sobre duas colunas retangulares com 6m de altura, de largura 20cm e altura 45cm. O fck do concreto é 25 Mpa.

Nossa missão é determinar corretamente quais as reações de apoio devemos passar para o nosso colega que vai calcular as colunas de concreto armado.

Passo 1: calcular o módulo de elasticidade secante do concreto

E_{cs}=0,085 . 5600 . \sqrt{f_{ck}}

E_{cs}=0,085 . 5600 . \sqrt{25} = 2380 \space kN/cm²

Passo 2: Calcular a rigidez K da coluna

K = \frac {E_{cs} . B. A³} { 4L³} 

K = \frac {2380 . 20. 45³} { 4 . 600³} = 5,02 \space kN/cm

Passo 3: aplicar o coeficiente de mola calculado no apoio e obter as reações de apoio

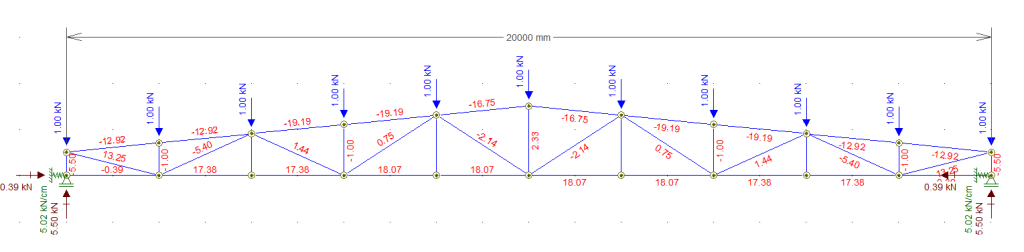
Após aplicar o coeficiente de mola nos dois apoios, obtivemos então uma reação de apoio horizontal de valor igual a 0,39 kN e uma reação de apoio vertical de 5,50 kN. E esses são os valores que devemos passar para nosso colega que vai calcular o concreto armado

Dessa forma ele vai concluir que a coluna será submetida a um esforço de compressão (vertical) igual a 5,50 kN, um esforço cortante (horizontal) igual a 0,3933 kN e um momento fletor igual a 0,3933 x 600 = 236 kN.cm

Caso tivéssemos passado os valores obtidos com os apoios de segundo gênero sem qualquer consideração de rigidez, teríamos uma força horizontal de 14,5 kN, vertical de 5,50 kN e isso geraria nas colunas uma compressão de 5,50 kN, um esforço cortante de 14,50 kN e um momento fletor de 8700 kN.cm (3718% superior ao encontrado usando os coeficientes de mola!!!).

Mas como podemos checar se esses resultados estão corretos?

Para demonstrar se nosso cálculo está correto podemos simplesmente inserir a coluna de concreto no modelo do ftool e checar se os esforços estão coerentes com os resultados obtidos pelo cálculo acima, da seguinte forma:

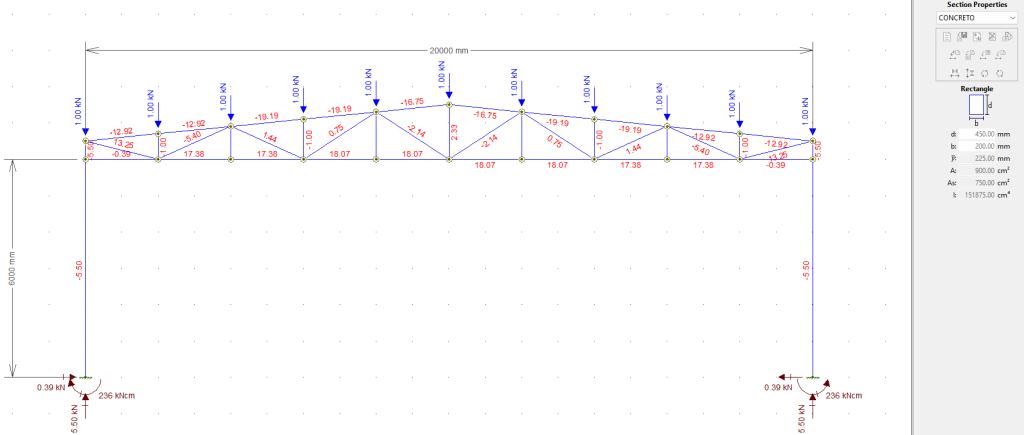
Inserindo uma coluna retangular com seção 450mm X 200mm, com módulo de elasticidade igual a 23800Mpa (equivalente a 2380 kN/cm²) obtivemos exatamente os mesmos esforços na treliça, validando assim nosso cálculo com apoios dotados de coeficiente de mola: Compressão de 5,5 kN, momento fletor de 236 kN.cm e cortante de 0,39 kN.

E assim você não precisa mais brigar com o colega calculista do concreto armado, basta enviar para ele as reações de apoio dessa forma e tudo ficará bem resolvido

Espero que esse artigo tenha te ajudado. Se ajudou, envie para alguém que possa se beneficiar desse conteúdo. Se você tem alguma dúvida sobre o que foi tratado, poste aqui nos comentários. Se esse artigo for bem recebido posso fazer um vídeo a respeito.

Não se esqueça de conferir a bibliografia recomendada e bons estudos!

Eng. Felipe Jacob