Tutorial de Ftool para estruturas metálicas

Sejam muito bem vindos mais uma vez ao blog do Calculista de Aço, aqui quem vos fala é o Eng. Felipe Jacob e hoje trago até vocês um tutorial completo do ftool, um excelente software gratuito que foi desenvolvido dentro do instituto Tecgraf, na PUC-Rio, sob a supervisão do professor e escritor Eng. Luiz Fernando Martha e é atualmente o software free mais popular entre calculistas e estudantes.

Para que serve o Ftool?

O ftool é um programa que nos permite realizar a análise linear elástica de estruturas compostas por barras unifilares contidas em um plano. Explicando de maneira bastante simplista, é uma ferramenta que nos possibilita extrair informações importantes como deslocamentos, deformações, esforços e reações em uma estrutura plana.

Portanto é importante ficar claro desde o início que não é possível dimensionar um estrutura metálica somente usando o ftool, pois ele só nos atende na etapa de modelagem e obtenção dos esforços. Depois disso ainda é necessário verificar se a estrutura está aprovada quanto aos deslocamentos máximos previstos (Estados Limites de Serviço) e quanto às resistências de projeto estabelecidas pelas normas aplicáveis (Estados Limites Últimos). Se você não tem a menor ideia do que são Estados Limites Últimos ou Estados Limites de Serviço, é melhor ver essas 4 aulas gratuitas do meu curso antes de tentar calcular qualquer coisa.

Já na segunda etapa, o ftool não nos ajuda em mais nada, mas podemos elaborar os cálculos manualmente ou utilizar algumas ferramentas automatizadas como Visual Metal, DimPerfil, ou então com esta planilha que eu desenvolvi.

Mas observe que essas ferramentas não cobrem todos os tipos de perfis que podem ser calculados, então é fundamental que o profissional tenha conhecimento a respeito dos roteiros de cálculo exigidos pela NBR8800/08 e NBR14.762/10.

Agora que você já sabe o que o programa pode fazer e principalmente o que não pode fazer, vamos em frente com nosso tutorial de ftool.

Baixando o Programa

1 – Acesse o site https://www.ftool.com.br/Ftool/

2 – Um vez no site clique no botão “Download”

3- Clique no botão “Register”

4 – Nessa tela você deverá fazer um cadastro, após concluir envie o formulário e você será redirecionado à tela de login.

5 – O Ftool possui a opção de simplesmente baixar o arquivo e utiliza-lo de forma gratuita, ou comprar uma licença anual. Você consegue fazer qualquer cálculo com a versão gratuita, mas a versão avançada tem alguns recursos interessantes, como a possibilidade de lançar diversas combinações de cargas em um mesmo arquivo, deixar gravado suas unidades favoritas e a mais legal de todas é um editor de perfis onde você consegue criar um perfil personalizado através de coordenadas. Como eu disse, você não precisa disso para fazer seus cálculos, mas são recursos bacanas.

6 – o Software é bastante leve e não requer instalação, bastando extrair o arquivo Zip para uma pasta qualquer e rodar o arquivo ali mesmo.

Primeiros Passos

Se você estiver usando a versão gratuita, será necessário configurar o sistema de unidades todas as vezes que abrir um novo projeto. para isso clique no menu “Options > Units & Number Formatting”:

Eu gosto de usar o programa nas seguintes configurações:

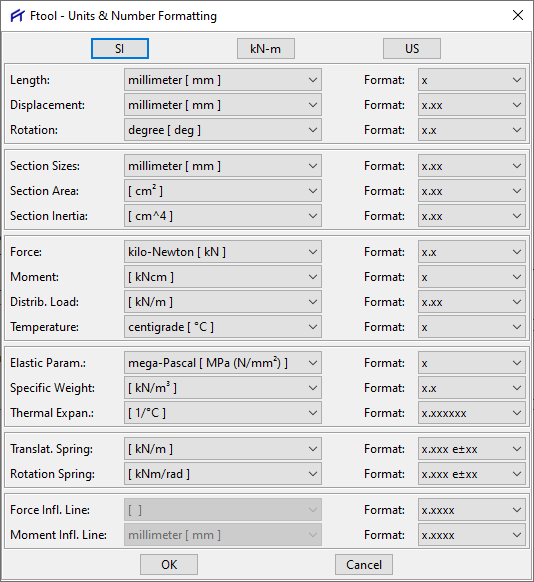
Essa configuração nos permite extrair os esforços de maneira mais limpa e prática, além de facilitar as consultas a tabelas de perfis quando estivermos fazendo os cálculos de resistência.

Criando a primeira barra através de coordenadas

No ftool é possível introduzir as barras de forma livre ou através de coordenadas. Para isso, devemos habilitar ou desabilitar o ícone do teclado na lateral esquerda da interface do programa:

Vamos criar nossa primeira barra através de coordenadas. Primeiro clique no ícone “Insert Member (M)” na mesma barra lateral. Você também pode simplesmente digitar “M” que o software automaticamente reconhece o comando.

Você será solicitado a introduzir coordenadas das extremidades da barra que você deseja introduzir. Neste primeiro exemplo criaremos uma barra com as coordenadas iniciais x = 0 e y = 0 (portanto, o primeiro nó da barra é na origem do modelo) e coordenadas finais x = 1000mm e y = 1500mm:

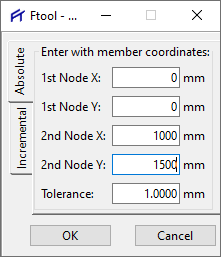
Após clicar em OK, a barra que desejamos será plotada no espaço de trabalho do programa:

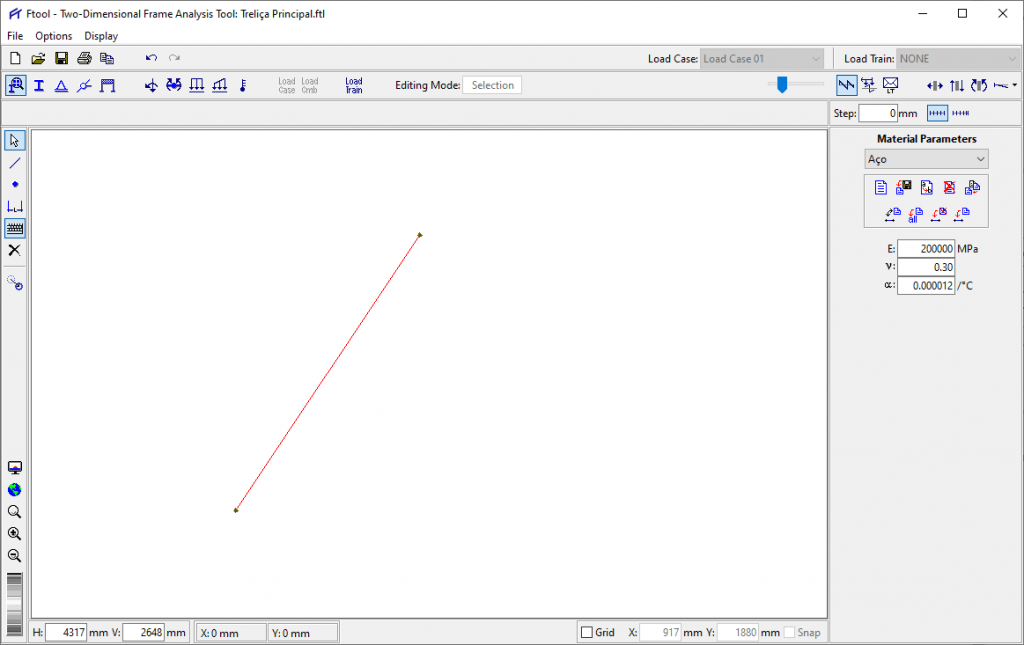
Observe que no canto inferior esquerdo aparecem algumas informações:

• H é a largura e V é a altura do zoom que está sendo visto na tela do Ftool. Esse valor será alterado quando você aumenta ou reduz o zoom da tela girando a rodinha do mouse.
• X e Y indicam a posição do cursor do mouse na tela. Se você passar o cursor no nó inferior, vai obter as coordenadas X=0 e Y=0, e se colocar o cursor sobre o nó superior, vai obter as coordenadas X = 1000 mm e Y = 1500 mm, como havíamos especificado anteriormente.

Podemos cotar nossa barra utilizando a ferramenta específica no canto esquerdo do programa. Para isso primeiro desative o modo de introdução por coordenadas clicando no ícone do teclado novamente e depois clique no ícone de uma linha de cota, como abaixo:

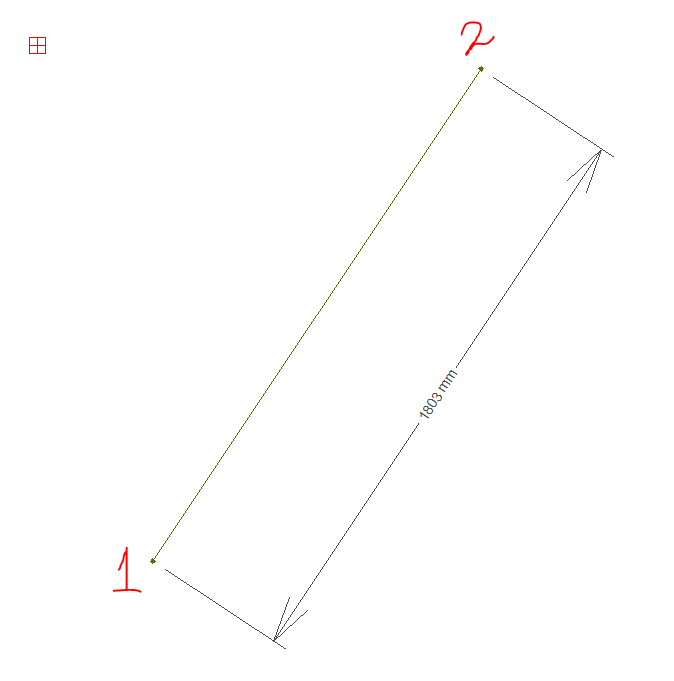
Após clicar no ícone de cota, clique no nó inferior e depois no nó superior e por fim afaste um pouco da linha, finalizando com um clique para obter a medida desejada.

Criando múltiplas barras através de coordenadas

É possível criar múltiplas barras através do sistema de coordenadas, sem necessariamente ter que introduzir as coordenadas uma a uma. Vamos supor que queiramos criar uma viga horizontal de 6000 mm de comprimento, dividia em 4 partes de 1500 mm. Para realizar essa tarefa de forma simples, vamos criar um primeiro trecho de 1500mm com as coordenadas iniciais x = 0 e y = 0, porém na aba “Absolute” da caixa de diálogo de coordenadas.

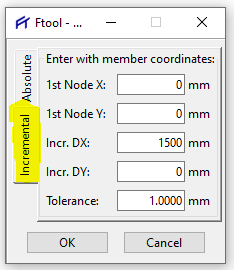
Ao clicar em “OK” uma vez, observe que foi criada uma barra horizontal, de 1500 mm exatamente como prevíamos:

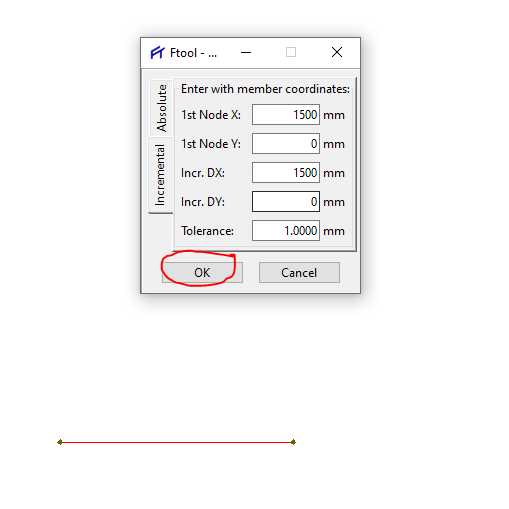
Porém, se você clicar mais 3 vezes em “OK” veja o que acontece:

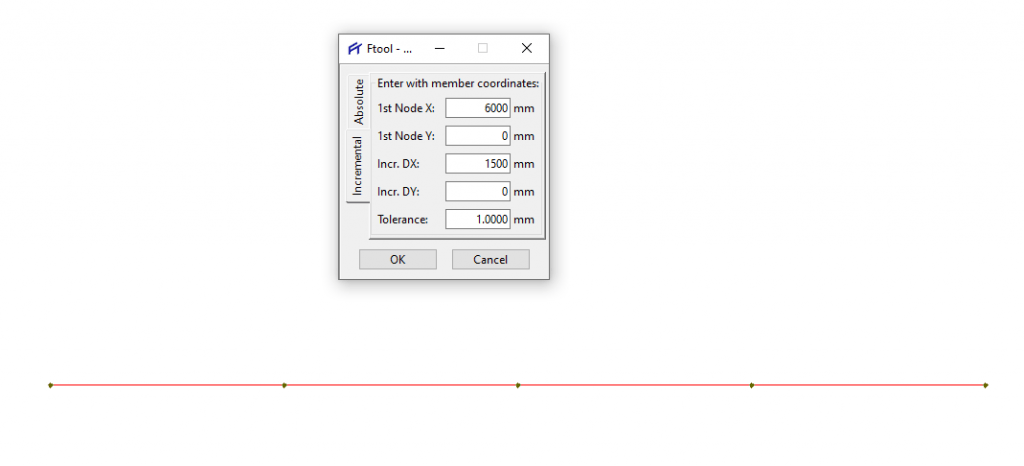
Foram criados mais 4 segmentos de reta, com 1500 mm cada um, onde o ponto inicial de uma barra é justamente o ponto final da outra. E assim temos a barra de 6000 mm horizontal que desejávamos.

Criando barras através do GRID e SNAP.

Eu, particularmente, não gosto de operar o ftool à partir do método de copordenadas, mas prefiro lançar as barras utilizando os recursos “Grid” e “Snap”. Quem tem alguma vivência com projetos em Autocad 2D já sabe do que eu estou falando.

Funciona da seguinte forma: Ao invés de introduzir as coordenadas uma a uma, barra por barra, o que fazemos é introduzir alguns pontos virtuais formando uma malha nas medidas desejadas na tela com clicando na opção “GRID” e depois obrigamos o programa a só navegar através desses pontos marcando a opção “SNAP”. Dessa forma conseguimos a mesma precisão das coordenadas, porém de uma forma um pouco mais ágil.

Vamos a um exemplo: vamos desenhar uma treliça reatangular com altura 1100 mm, comprimento 8000 mm e montantes a cada 500 mm.

Primeiro, no canto inferior direito da tela, marque as opções GRID e SNAP, e introduza as coordenadas X = 8000 mm e Y = 1100 mm como opções (Não se esqueça de desmarcar a opção de introdução por coordenadas, clicando sobre o ícone do teclado na margem lateral esquerda do programa):

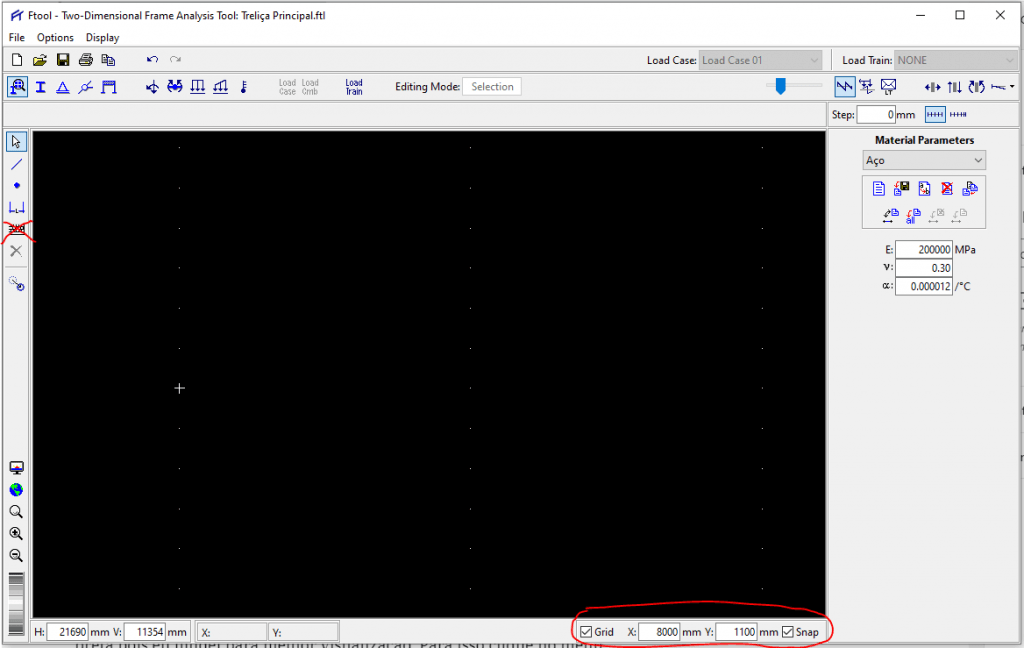
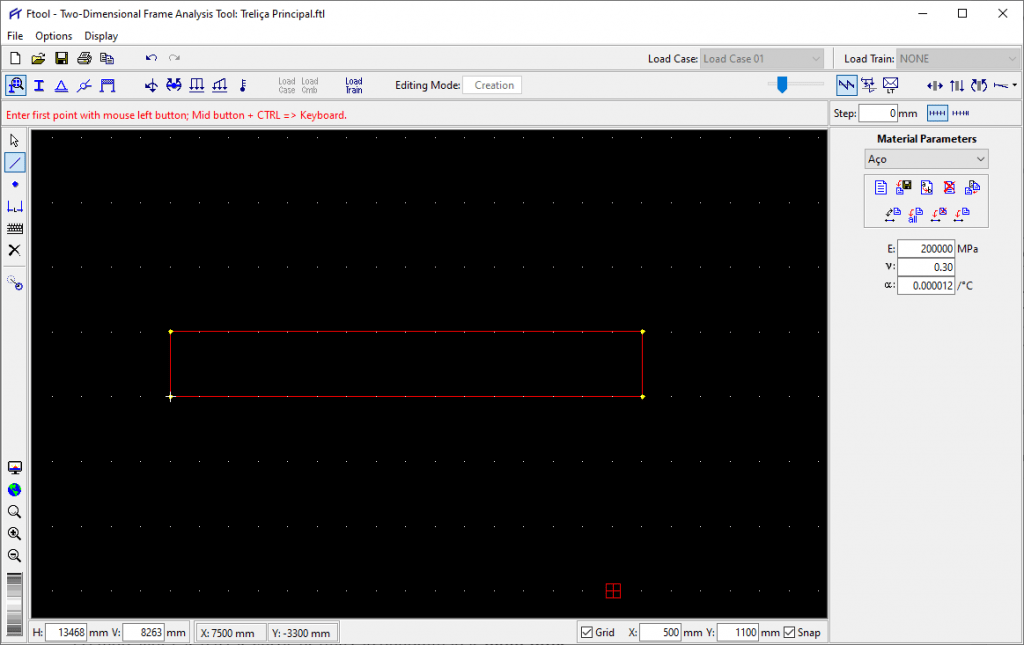
Observe que foram criados pequenos pontos na tela (a tela do exemplo está preta pois eu mudei para melhor visualização. Para isso clique no menu superior “Display > Black Background”), sendo que a distância horizontal entre eles é sempre 8000 mm e a distância vertical é sempre 1100 mm. Ao marcar a opção SNAP também determinamos ao programa que o cursor só poderá repousar sobre esses pontos, e com isso podemos criar o contorno externo da nossa treliça simplesmente clicando sobre os pontos que o programa nos permite visitar.

Clique no ícone para criar barras, depois clique em cada um dos pontos que representam o contorno externo da sua treliça:

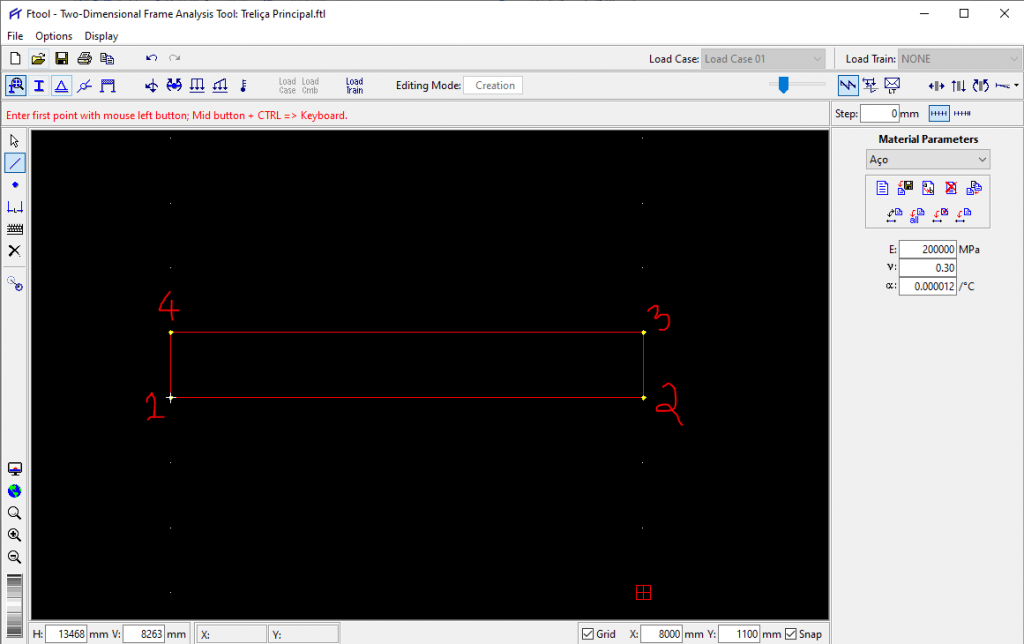
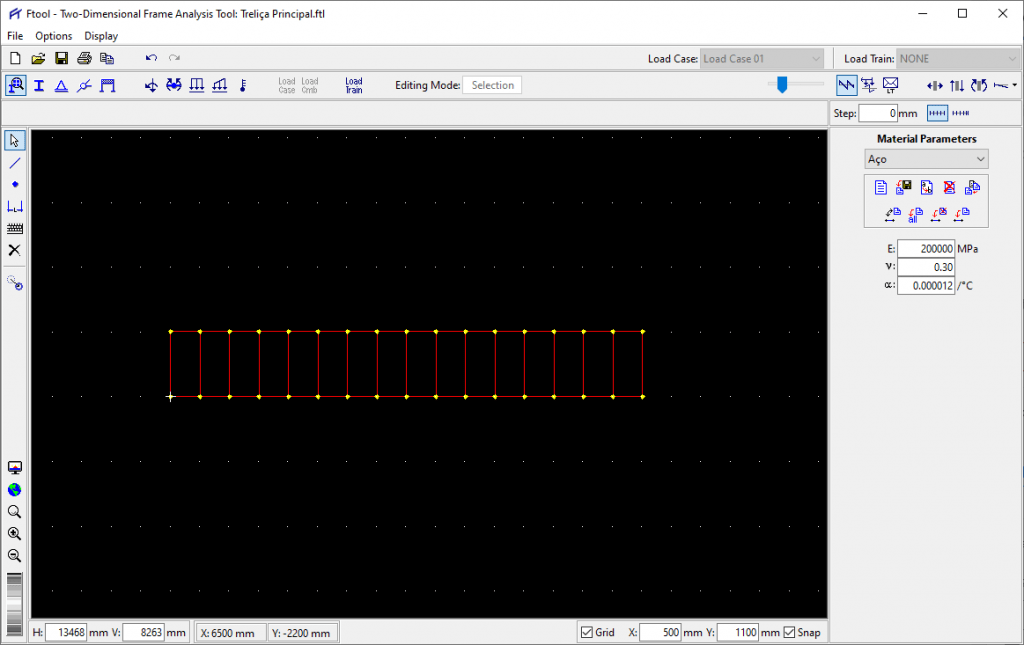
Agora que o contorno está definido, vamos criar os montantes a cada 500 mm. Para isso altere o GRID para x = 500 e y = 1100 e repita o procedimento, criando agora as barras verticais que são denominadas montantes.

Agora se quiser pode desligar o Snap, e basta então clicar sobre os nós que foram criados para criar as diagonais da treliça. Nesse caso vamos fazer uma treliça tipo Pratt que é bastante indicada para vigas treliçadas que só recebem cargas verticais em uma só direção.

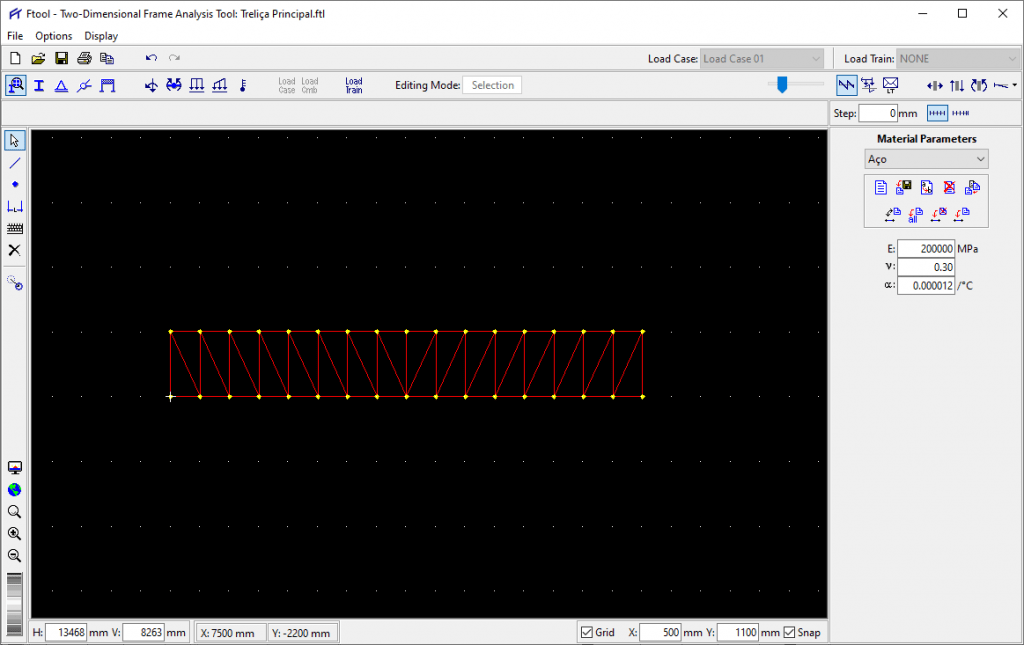
Observe que até o momento, apenas estamos definindo a geometria da treliça. Ainda não introduzimos os perfis, nem os apoios e nem o material da qual ela é composta, mas por enquanto vamos continuar explorando as ferramentas de modelagem.

No segundo exemplo vamos criar uma treliça de duas águas com vão livre teórico de 16000 mm, altura de cumeeira de 1300 mm e alturas das laterais de 500mm, com montantes a cada 1000 mm e diagonais alternadas.

Primeiro, vamos elaborar o contorno. Mude o GRID para x = 8000 e y = 1300, e crie o banzo inferior e o montante central.

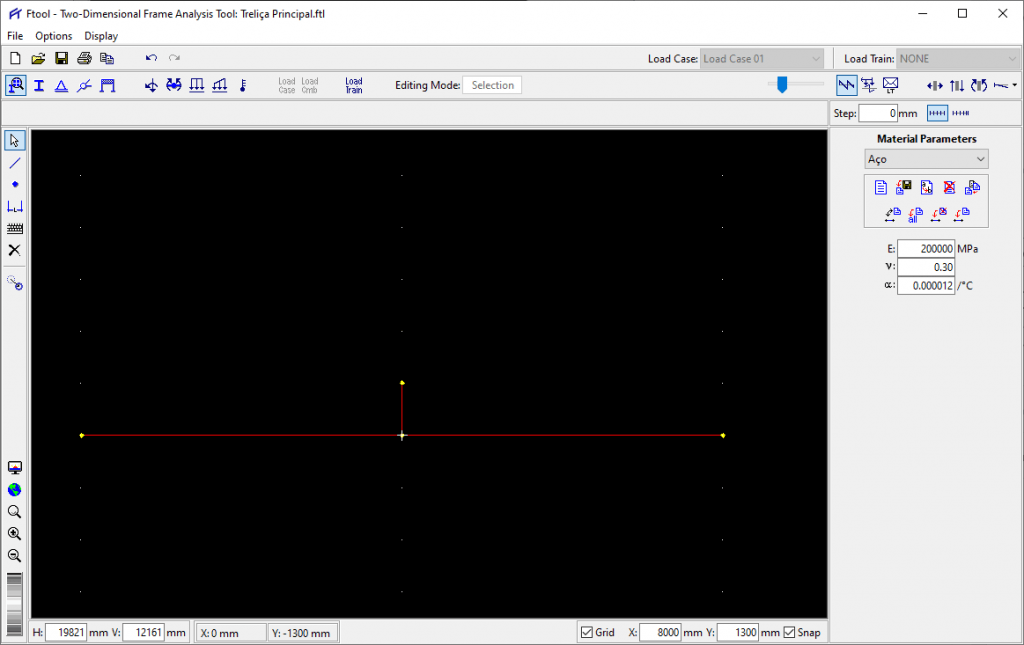
Agora altere o GRID para x = 8000 e y = 500 e complete o contorno. Pode ser necessário desligar o SNAP pois o nó da cumeeira não coincide com o GRID, portanto sempre que precisar pegar em algum ponto fora do GRID, desligue o SNAP e depois volte a ligá-lo novamente.

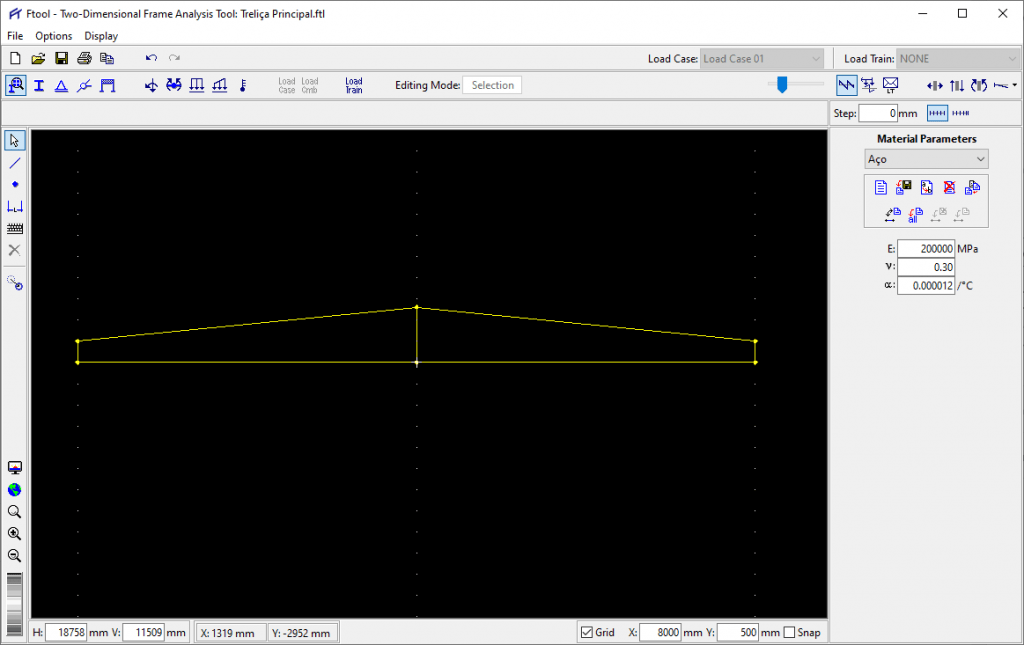
Agora vamos criar os nós dos montantes. Para isso vamos alterar o grid para x = 1000 e y = 3000. Observe que vamos adotar uma cota de Y maior do que a altura da treliça, pois vamos criar barras que ultrapassem a treliça totalmente de pois vamos remover os excessos.

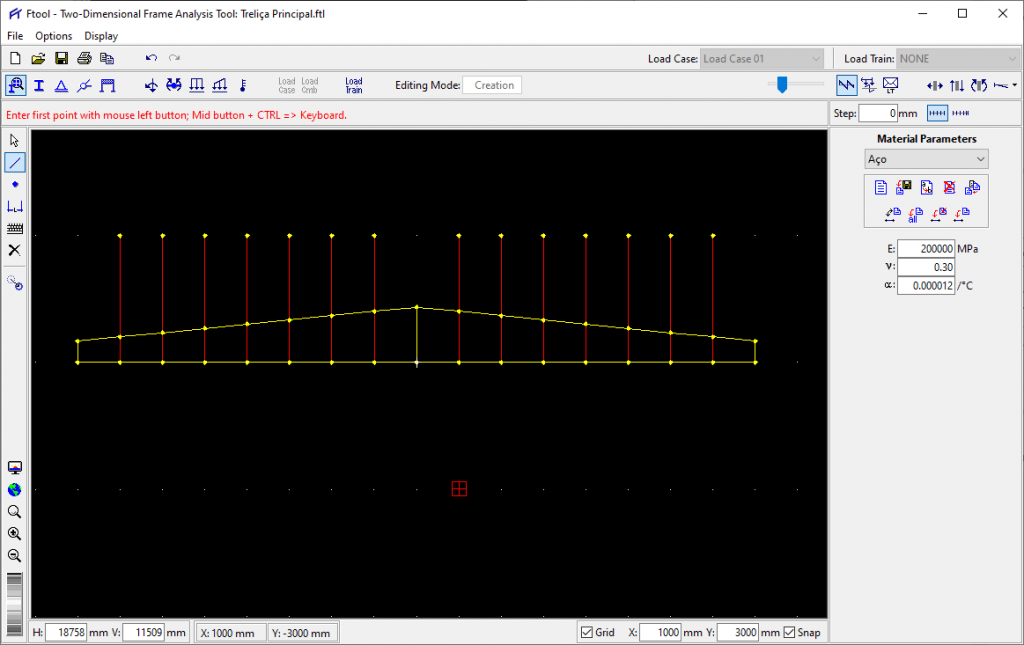
para remover os excessos basta selecionar a ferramenta da seta, logo acima do ícone que usamos para criar barras, clicar sobre os trechos que desejamos remover e pressionar Delete. Aqui também vale a mesma regra do AUTOCAD: Se selecionarmos as barras da direita para a esquerda, tudo o que o mouse tocar será selecionado, mas se selecionarmos da esquerda para a direita, somente as barras que forem totalmente cobertos pela seleção do mouse serão selecionados.

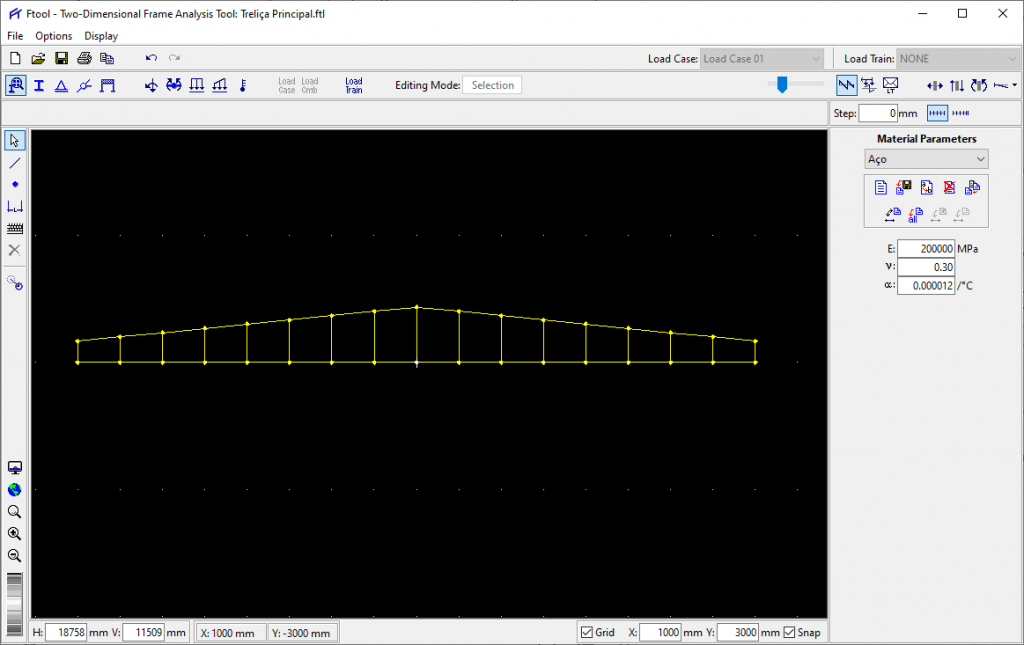
e por fim vamos finalizar com as diagonais

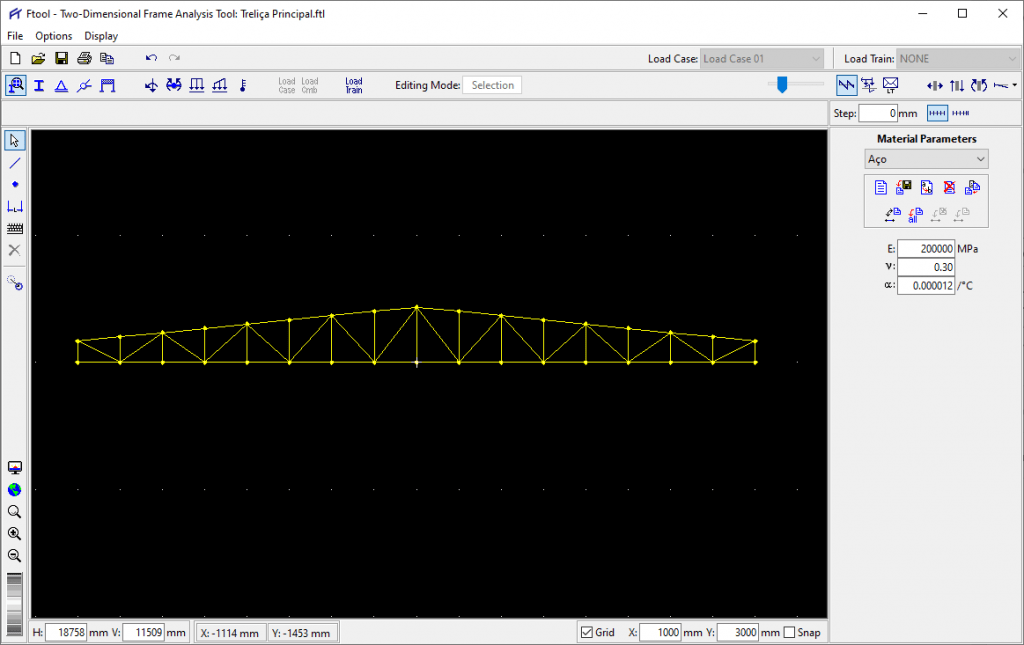
Comandos Move, Rotate, Scale e Mirror

Agora vamos explorar algumas ferramentas que facilitam bastante nossa vida na hora de modelar a estrutura. Primeiro você deve habilitar o modo “transform”, que lhe habilitará realizar mudanças em várias barras ao mesmo tempo no modelo. para isso, clique no ícone “Transform” na barra lateral direita do programa:

Após clicar nesse ícone, uma tela diferente aparecerá no lado direito do software, mas por enquanto nenhuma ação é permitida pois você deve primeiro selecionar as entidades que quer modificar. Vamos selecionar toda a treliça (Após a seleção, as barras mudam de cor).

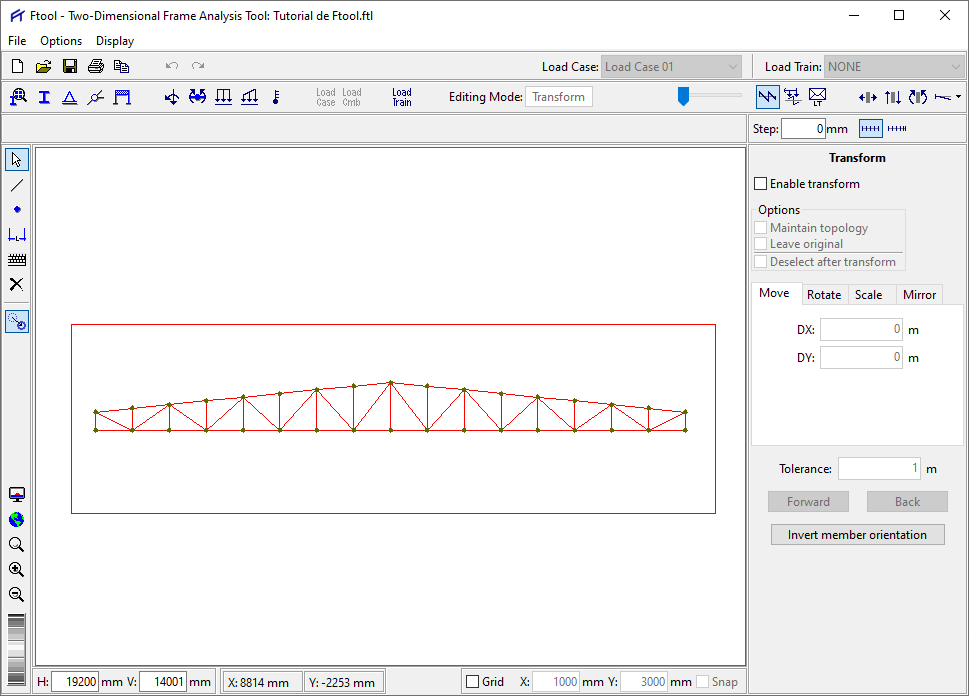
Após selecionar todas as barras, clicamos em “Enable Trasnform” na tela que se abriu à direita do programa e então o software vai nos permitir selecionar algumas opções. Observe que temos as seguintes abas:

• “Move” – Permite deslocar o conjunto selecionado no campo da tela
• “Rotate” – Permite rotacionar o conjunto selecionado em torno de um ponto fixo
• “Scale” – Aumenta ou diminui o conjunto com base em um fator
• “Mirror” – Permite espelhar o conjunto selecionado.

Observe que logo acima dessas abas temos algumas opções

• “Maintain Topology” – Quando esta opção está desativada, a mudança só ocorre quando houver um segundo clique do mouse. Por exemplo, se você mantiver essa opção desativada, com “enable transform” ativado e a aba “move” selecionada, você poderá mover a seleção clicando sobre um ponto qualquer, movendo o mouse para a direção desejada e depois ao clicar novamente, o conjunto se move. Mas se você não der o segundo clique, e pressionar “Esc” antes disso, a seleção não se move, e volta para a posição original. O programa fica esperando um segundo clique para executar a ação. Por outro lado, se você ativar a opção “Maintain Topology”, isso ocorre dinamicamente e o programa atualiza a posição do objeto a todo momento, ou seja, não é necessário um segundo clique para que ocorra o movimento, e se você não der o segundo clique e pressionar “Esc”, a seleção ficará onde o mouse estava parado. Esse não é o único efeito dessa opção. Ao deixá-la selecionada, o programa impede que uma barra atravesse outra, impedindo assim a cruzamento entre barras já existentes no modelo. Eu particularmente não vejo muita utilidade nessa função, mas alguém pode gostar, então está aí a explicação do que ela faz.
• “Leave Original” – Quando essa opção está marcada, o programa cria uma cópia do que foi selecionado e deixa as barras originais no lugar. Não é possível marcar “Leave Original” e “Maintain Topology” ao mesmo tempo. “Leave Original” é uma ferramenta excelente para economizar tempo e evitar erros, pois podemos criar apenas parte de um modelo e utilizar esse recurso para mover, rotacionar e espelhar peças sem ter que ficar criando todas as barras uma a uma.
• “Deselect after transform” – Por padrão, quando essa opção está desmarcada, após a movimentação das peças selecionadas, o programa as mantém selecionadas e prontas para outra transformação. Se você marcar essa opção, após o movimento o programa remove a seleção. Outra opção de pouca utilidade prática.

Vamos criar uma cópia da nossa treliça:

1 – Selecione toda a treliça é que todas as barras mudem de cor, e marque a opção “Enable Transform”, e também a opção “Leave Original”. Deixe as outras opções desmarcadas.

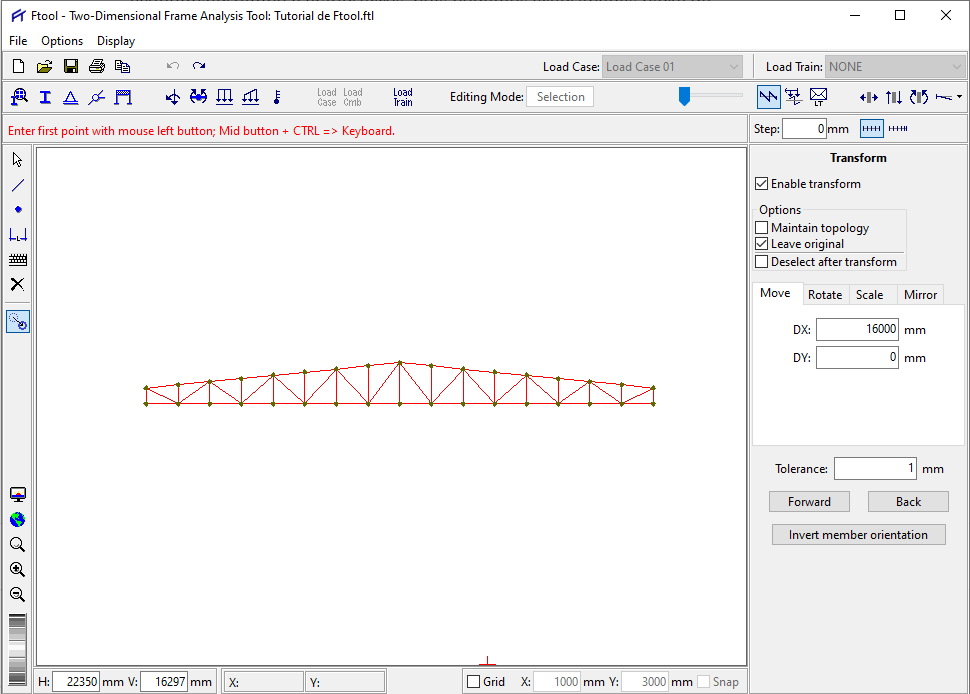
2 – Depois disso, clique em um ponto qualquer da treliça e mova o mouse para a posição desejada. Aqui vale a pena utilizar o GRID e o SNAP, ou então utilizar pontos da própria estrutura como referência. Vamos criar uma treliça de quatro águas, colocando o ponto inferior esquerdo alinhado com o ponto inferior direito da treliça, criando assim uma cópia.

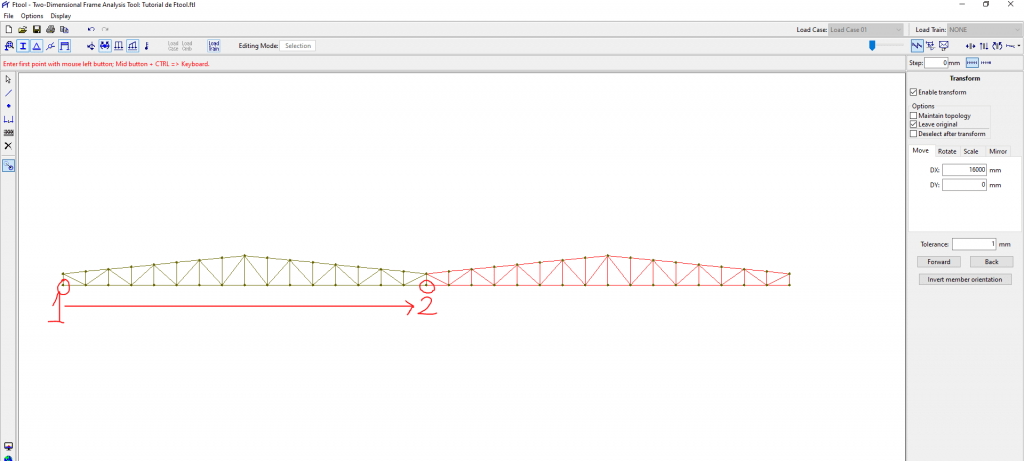
É importante ressaltar que o zoom deve estar amplo, pois o programa apresenta um bug onde somem algumas barras após a cópia. Portanto deixe o zoom o mais próximo possível mas que ainda seja suficiente para que a cópia apareça totalmente na tela.

Pronto, temos um treliça de quatro águas.

Vamos agora criar uma treliça de duas águas, à partir de uma única água usando o comando “Mirror”.

1 – Apague todas as barras e deixe somente uma água no modelo, selecione as barras, ative o “Enable Transform”, “Leave Original” e selecione a aba “Mirror”:

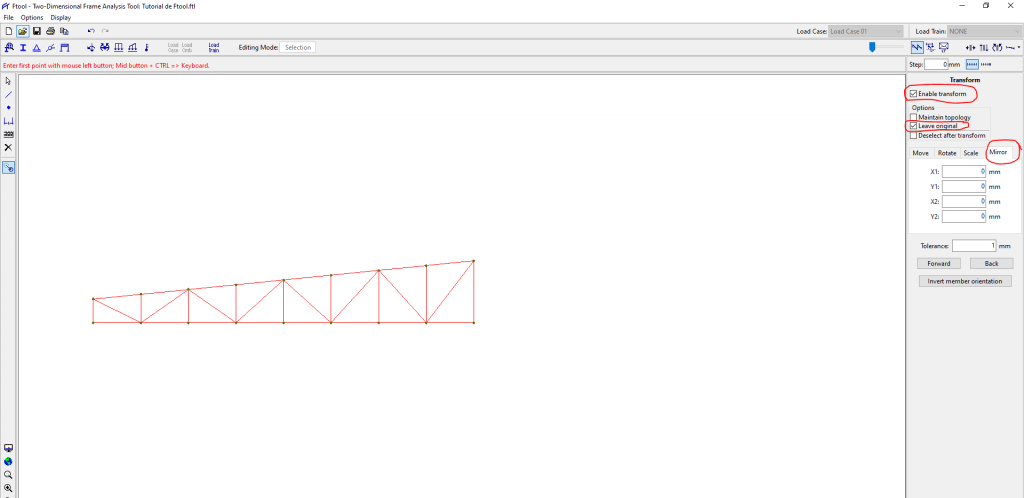
2 – Selecione o ponto superior do montante da cumeeira e depois o ponto inferior desse mesmo montante. A seleção pode ser inversa também. Apenas tenha em mente que a linha criada pela seleção representa a face de um “espelho imaginário” e que a imagem a ser criada é o reflexo desse espelho.

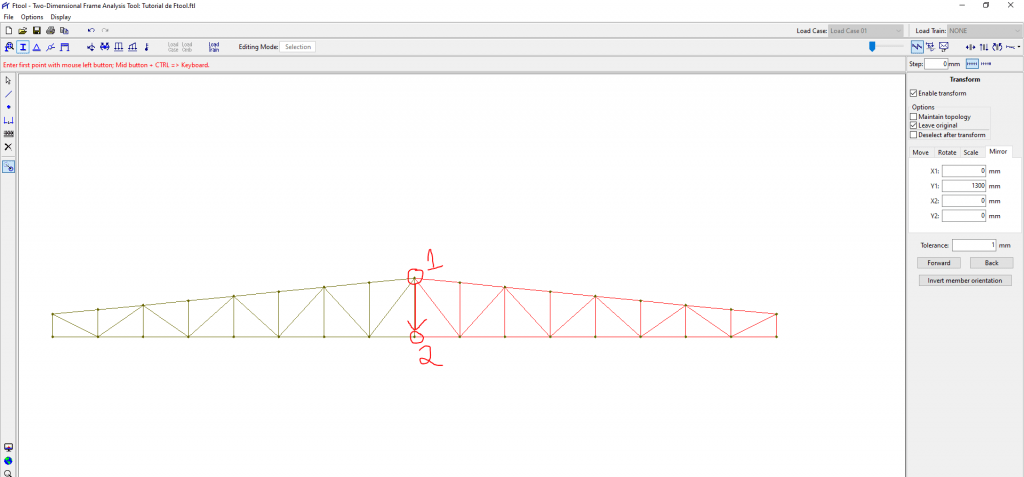
Pronto, temos uma treliça de duas águas criada à partir do espelhamento. Podemos fazer isso com galpões, coberturas, mezaninos, enfim, qualquer estrutura simétrica.

As abas “Rotate” e “Scale” funcionam sob a mesma lógica, mas não possuem muita utilidade quando marcada a opção “Leave Original”, servindo apenas para rotacionar ou escalar um modelo. O comando “Scale” particularmente é raramente usado e o comando “Rotate” é intuitivo, bastando selecionar o modelo, escolher um ponto de referência que será o ponto de giro e indicar o ângulo desejado.

Exportando um modelo para DXF, PDF e outros formatos.

Muitas vezes é interessante exportar o modelo criado para iniciarmos um detalhamento no Autocad ou outra ferramenta que seja capaz de ler arquivos DXF, ou mesmo gerar um PDF com as informações básicas do modelo para documentar um memorial de cálculo.

Infelizmente o contrário ainda não é possível ser feito, ou seja, não conseguimos criar um modelo no no Autocad e depois importar para o Ftool, algo que nos pouparia certo trabalho de modelagem, principalmente para aqueles usuários avançados de Autocad que dominam recursos avançados de modelagem no programa, como uso de arrays.

para exportar o desenho para DXF, clique em “File> Export Screen > DXF”:

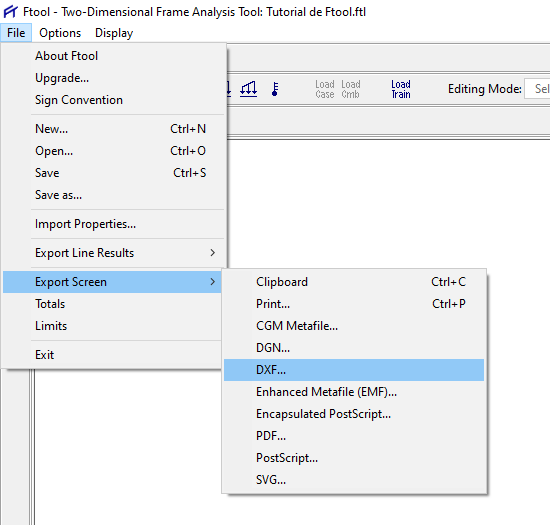
Selecione a pasta na qual deseja salvar o arquivo e então abra o mesmo.

Observe que o modelo não vai na escala certa com as cotas colocadas no Ftool, mas vai nas medidas do zoom (???). Portanto é necessário que você ajuste essa escala no Autocad se quiser ter um modelo condizente com o projeto real. (ou talvez exista uma forma de exportar com as cotas corretas e eu não tenha descoberto ainda. Se existe uma forma e você sabe, poste nos comentários por favor).

Para acertar essa escala, basta medir com a cota do Autocad qualquer medida conhecida e depois escalar. Por exemplo, sabemos que o banzo inferior deve medir 16000 mm. Se ao cotar, encontramos 8368 mm, nossa tarefa é escalar o modelo em 16000 / 8368 = 1,912.

Atribuindo as propriedades de material

Até agora o ftool não sabe se nossa treliça é de aço, de madeira, plástico, bambu ou qualquer outro material. Para isso é necessário informar ao programa o material do qual as barras são feitas. Como esse tutorial se refere ao uso do Ftool para estruturas metálicas, vamos atribuir o material aço.

1 – Clique no ícone “Material Parameters”, localizado no conto superior esquerdo do programa.

2 – No painel direito surgirá um menu onde devemos realizar algumas ações. A primeira coisa que devemos fazer é criar um novo material clicando no ícone “Create New Material Parameters”, conforme abaixo:

3 – Na caixa denominada “New Label” precisamos dar um nome para esse material. Aqui chamaremos de “Aço” e colocaremos a caixa de seleção na opção “Steel Isotropic”:

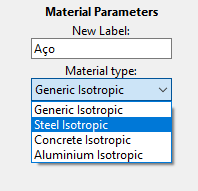
4 – Logo surgirão as propriedades básicas que o programa precisa saber sobre o material. Por padrão no Ftool o Módulo de Elasticidade é 205.000 Mpa, porém de acordo com a NBR8800 esse valor é 200.000 MPa. A diferença no final dos cálculos é muito pequena e na prática não tem influência significativa nos resultados, mas você pode alterar esse campo se quiser que seu modelo seja fiel ao texto normativo. Os outros parâmetros se referem ao Coeficiente de Poisson e ao coeficiente de dilatação térmica, que podem ser deixados como estão.

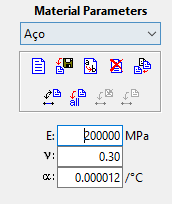
6 – Agora precisamos selecionar todas as barras e dizer para o programa que aquelas barras são do material de acabamos de criar. Para isso, após a seleção das barras, clique no ícone “Apply Current Materials to Selected Members”:

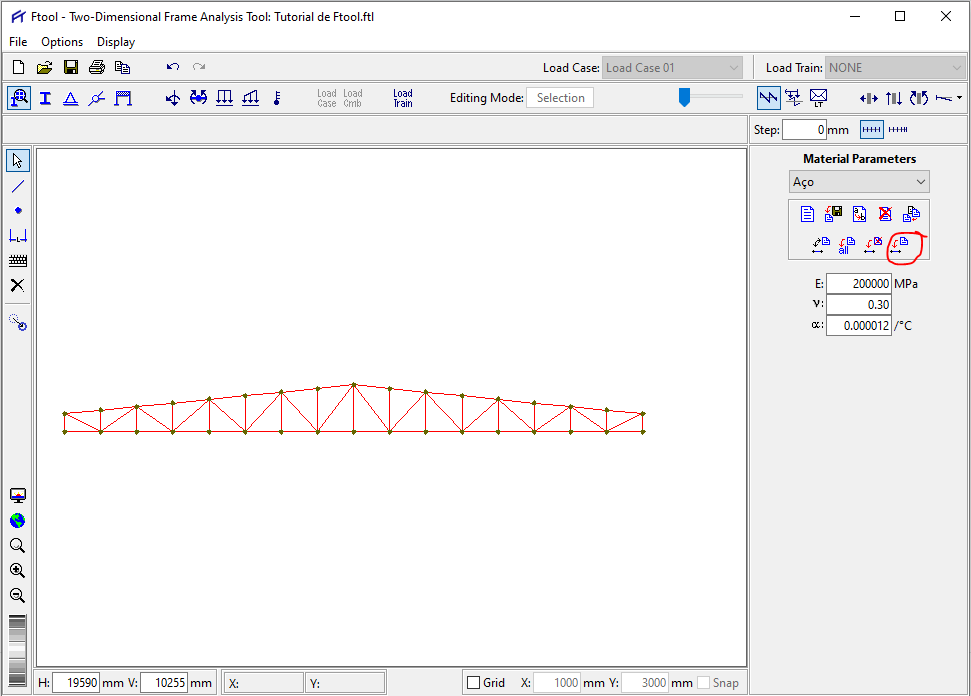
Pronto, agora o programa sabe que todas essas barras possuem as propriedades mecânicas referentes ao comportamento elástico do aço.

IMPORTANTE

Observe que não introduzimos algumas outras propriedades como o limite de escoamento ou limite de ruptura, que também são propriedades mecânicas. Isso acontece pois, como foi mencionado anteriormente, o programa ftool só nos auxilia na análise linear elástica, ou seja, ele não nos dá condições de saber se o material sofreu escoamento, flambagem, ruptura ou qualquer outro fenômeno relacionado à resistência do material. Para o ftool, todas as barras são infinitamente elásticas e podem se deformar indefinidamente, e ele sempre vai considerar que o material está dentro do regime elástico. Cabe ao calculista fazer as verificações adequadas para saber se o material realmente permanece no regime elástico e se nenhuma deformação indesejada ocorreu. Essas verificações são chamadas Estados Limites Últimos, e são realizadas com outras ferramentas ou mesmo manualmente aplicando os textos das normas específicas (Para estruturas de aço são a NBR8800 e NBR14.762, existem outras para estruturas específicas como Porta Pallets NBR15.524 e Equipamentos de Movimentação, como pontes rolantes e monovias NBR8400).

Se você quiser aprender como realizar essas verificações de maneira correta, eu tenho um curso completo de projeto e cálculo de estruturas metálicas no site www.calculistadeaco.com.br onde você aprende a calcular estruturas metálicas desde o básico, começando pelos cálculos manuais, depois com ferramentas totalmente gratuitas e por fim operando o Cypecad Metalicas 3D. Se você quer ter segurança para atuar nesse ramo, é necessário que você se dedique e aprenda a realizar as verificações manualmente para não ser refém de nenhum software que, apesar de facilitarem muito nossa vida, nem sempre soltam resultados corretos, como você pode ver nesse vídeo aqui:

Atribuindo a rigidez interna dos nós

Por padrão, inicialmente todos os nós criados no ftool são rígidos, ou seja, se uma barra tende a girar, ela carrega consigo e “tenta forçar” a outra barra também a girar. Porém em algumas situações, desejamos criar ligações flexíveis, que permitem o giro individual de cada peça de forma independente. Especialmente em treliças, é prática muito comum entre alguns calculistas atribuir nós flexíveis por considerarem que o comportamento final da treliça em nós soldados (teoricamente rígidos) é muito aproximado do comportamento da treliça com nós flexíveis, ignorando portanto o efeito dos momentos fletores locais que de fato são bastante pequenos quando medidos pelo programa. Eu não gosto muito dessa aproximação e prefiro simular o comportamento com nós rígidos mesmo que a diferença seja ínfima, mas como eu sempre digo, nenhum modelo matemático é capaz de representar com 100% de fidelidade a realidade no campo, e o calculista é responsável por determinar até que ponto suas aproximações ou considerações permanecem válidas e fiscalizar se o que está sendo executado se comporta adequadamente conforme o modelo que ele determinou. Portanto vou mostrar como se faz isso caso deseje seguir nessa linha.

1 – Selecione todas as barras.

2 – Depois clique no ícone descrito abaixo:

3 – Na tela que aparece ao lado, selecione a opção “Articulate both member ends” e depois clique em “Apply hinge configuration to selected members”. Essa ação fará com que ambas as extremidades da barra sejam de nós articulados e portanto quando rodarmos o cálculo, os momentos fletores serão neutralizados, sobrando somente esforços de tração e compressão. Veja que existem outra opções bastante intuitivas, e se você quiser voltar com as ligações rígidas, basta então selecionar a opção “Remove hinge from both member ends” e de pois aplicar.

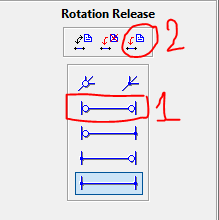
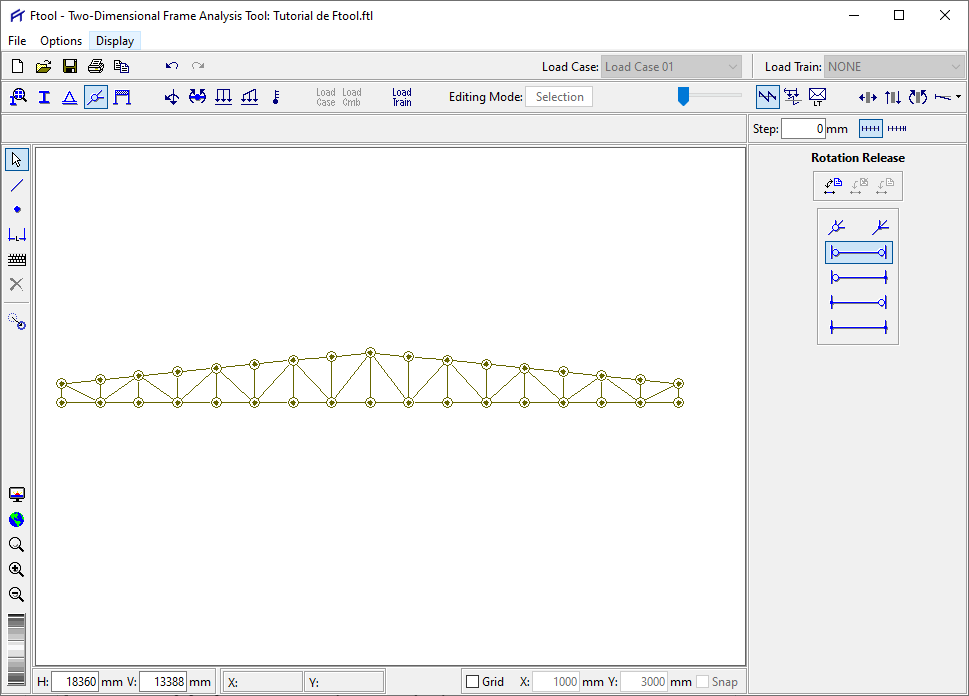
4 – Seu modelo deve ter a seguinte aparência depois de articular todos os nós:

Atribuindo apoios externos

Agora vamos dizer ao programa quais são os apoios externos da nossa treliça. Para isso, selecione os nós que deseja apoiar, segurando SHIFT e depois clique no ícone de apoios, conforme imagem abaixo:

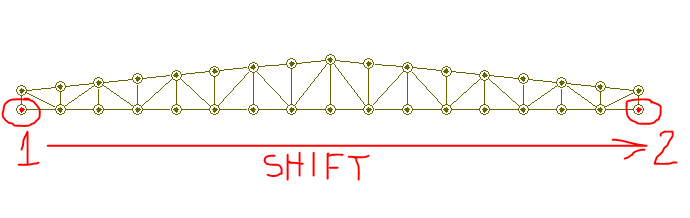
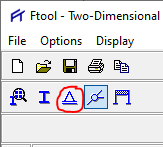
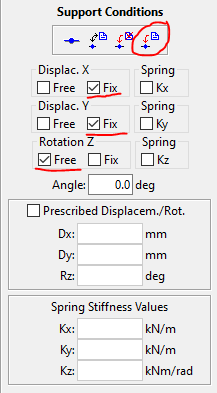
Na tela que se abrirá ao lado direito do programa, você poderá escolher os graus de liberdade dos apoios. Vamos Atribuir apoios de segundo gênero, ou seja, que possuem rotação permitida, porém translação impedida nas direções X e Y:

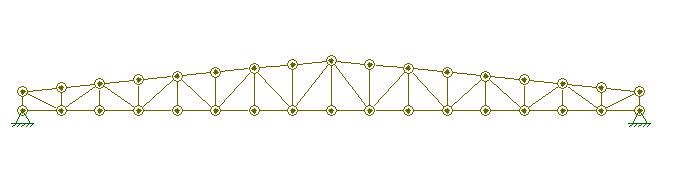
Feito isso, clicando em “Apply Current Conditions to selected nodes” o modelo deverá ficar assim:

Observe que selecionamos a opção “Fix” para os graus de liberdade X e Y, e “Free” para o grau de liberdade à rotação. Isso significa que com essas duas opções é possível criar apoios de rigidez perfeita ou liberdade perfeita, o que é muito comum por se tratar das condições extremas de apoio. Mas pode ser que você deseje criar apoios semi-rígidos, ou seja que não ofereçam resistência total em alguma direção. Isso é tarefa para calculistas experientes, mas se você souber o que está fazendo, basta selecionar a opção Spring na direção que deseja criar o apoio semi-rígido e informar a rigidez do apoio na caixa de diálogo “Spring Stiffness Values”, logo abaixo, com isso surgirá uma representação de mola no apoio indicando que ali há uma elasticidade prescrita.

Pode ser também que você deseje criar apoios que tenham certa mobilidade, mas não total. Para isso utilize a caixa “Prescribed Displacement / Rot.” e defina até que ponto cada nó pode se deslocar. Por exemplo, se você atribuir Dx = 15mm, no nó da esquerda, isso significa que quando o cálculo for efetuado, o nó direito poderá se movimentar 15mm para a esquerda ou para a direita atuando como nó livre nessa direção, sendo que se esse limite for atingido, passa a se comportar como nó rígido.

Atribuindo os perfis às barras

O programa já sabe qual é o material das barras, já sabe como as barras estão vinculadas internamente, como a estrutura está apoiada, agora nos resta determinar quais são os perfis das barras. Essa é uma parte de suma importância pois é preciso atribuir corretamente as direções dos perfis.

Vamos começar atribuindo um perfil U ao banzo superior.

1. Selecione somente as barras do banzo superior

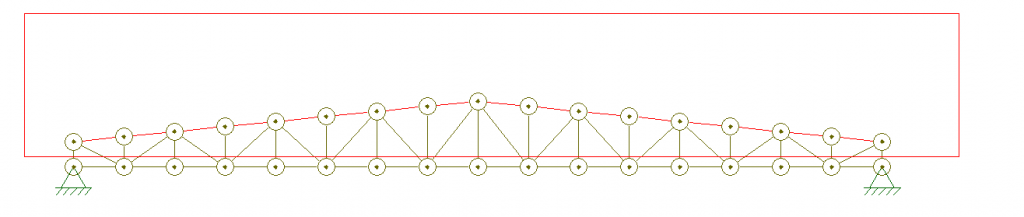
2. Depois clique no ícone de perfil I localizado no menu superior do programa

3. Feito isso, clique no ícone “Create new section Properties”, no menu que surge no lado direito do programa:

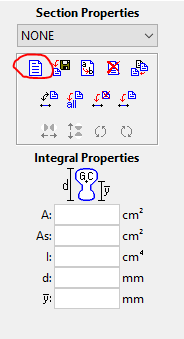
4. Dê um nome para o perfil e selecione o formato desejado. No exemplo nomeei como “Banzo Superior”. depois pressione “Done” na parte inferior deste mesmo menu.

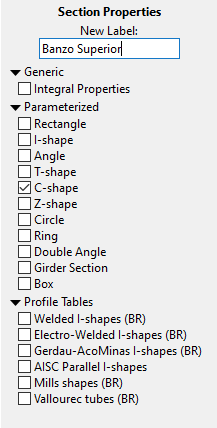
5. Na próxima tela será apresentado o perfil e sua orientação. É muito importante atribuir a orientação correta pois o programa utiliza o Momento de inércia em relação ao eixo horizontal da figura para realizar . DICA: Uma regra prática que sempre funciona é imaginar o que você veria se estivesse olhando a estrutura real de frente, e então imaginar um olho observando o perfil do ftool da direita para a esquerda (Veja a imagem abaixo). Esse olho representa o seu olho observando a estrutura. Se no banzo superior você vê a aba do perfil, então gire a peça até que o olho que você desenhou veja a aba do perfil. Se você vê a alma do perfil, mantenha ele em pé. No caso, como a treliça que estamos construindo terá o banzo superior em forma de U com a concavidade voltada para baixo então veremos a aba do perfil, portanto o perfil deve ser deitado conforme a imagem abaixo. Feito isso, não se esqueça de atribuir esse perfil clicando sobre o ícone “Apply current section to selected members”.

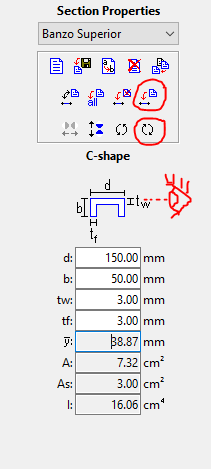
5. Vamos repetir o mesmo processo no banzo inferior, porém agora com o perfil deitado e voltado com a concavidade para cima. Mas não podemos simplesmente selecionar as peças do banzo inferior e girar o perfil que criamos, precisamos criar um novo perfil para esse banzo pois ao modificarmos o perfil denominado “Banzo Superior”, as peças que acabamos de fazer serão alteradas também

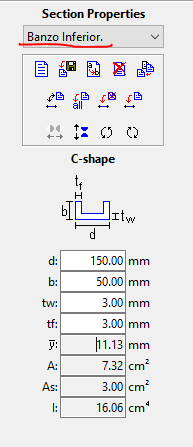
Assim finalizamos os perfis dos banzos.

Vamos iniciar a atribuição dos perfis das diagonais e dos montantes da estrutura. para agilizar o processo vamos usar um atalho para selecionar todas as diagonais sem precisar ficar clicando uma a uma.

Na tela de seleção de perfis coloque a caixa de diálogo em NONE, depois clique no ícone “Select Members by current section”

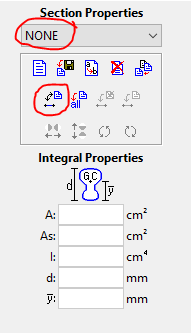
Isso fará com que todas as barras que não estiverem atribuídas a nenhum perfil sejam selecionadas. Isso é muito útil quando o ftool nos apresenta o erro “You must define section to all members”. O mesmo recurso também pode ser usado para materiais. Ao fim desse processo a tela deverá ficar assim (A tela está preta pois mudei o background para melhor visualização).

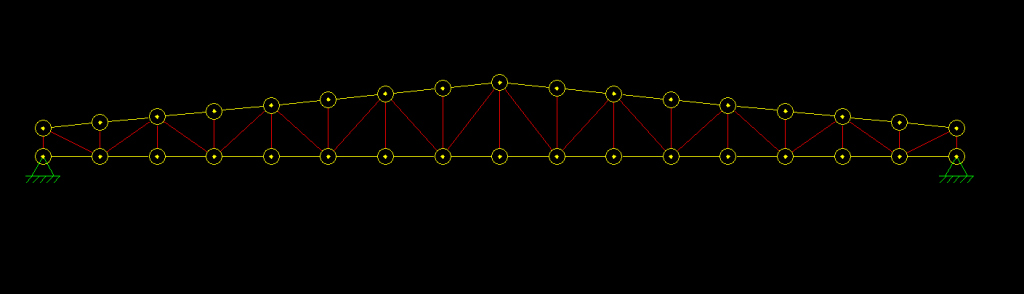
Agora vamos atribuir a essas barras um perfil de dupla cantoneira em formato de T. Para isso crie um novo perfil, selecione a opção “Double Angle” e coloque as propriedades, sempre prestando atenção para a orientação do perfil.

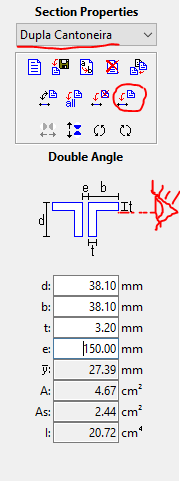
Observe que atribuímos a distância “e” como 150. na verdade, se o perfil estiver na orientação acima isso não fará diferença nos cálculos pois o programa só precisa do momento de inércia em relação ao eixo horizontal do perfil, faça você mesmo o teste alterando essa propriedade e verá que o último campo “I” permanece inalterado. Porém isso faz diferença se o perfil estivesse girado a 90°. Como o observador da treliça só é capaz de ver um dos perfis, sendo que o outro fica atrás, a orientação correta é a da imagem acima (Que pode ser para baixo ou para cima, como fizemos ali).

Gerando perfis que o ftool não tem em sua biblioteca.

Se você explorou a biblioteca de perfis que o ftool possui, deve ter notado que não existe, por exemplo, os perfis U enrijecidos, muito usados em terças de coberturas. O que fazemos nesses casos?

O programa possui um recurso que é a possibilidade de criar um perfil genérico, desde que você saiba quais são as propriedades corretas a se atribuir para ele. Para escolha o perfil desejado em uma tabela de perfis de um fabricante a sua escolha e depois crie no ftool um perfil Genérico “Integral Properties”.

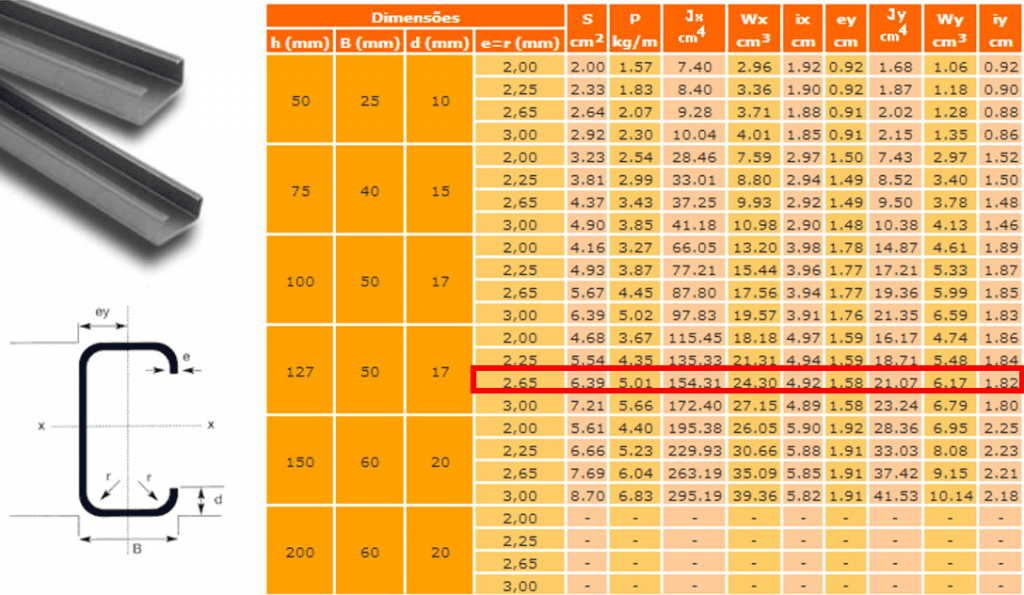
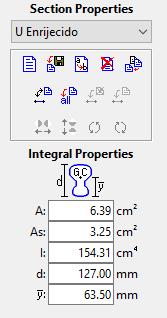
Nesse caso não é possível criar um perfil que possa ser girado, portanto devemos inserir as propriedades do perfil na posição que desejamos, e se quisermos ele girado, devemos criar outro perfil genérico. No caso acima criei um perfil U Enrijecido 127X50X17X2,65 em pé, como na figura do catálogo, portanto atribuímos os parâmetros:

1. Área da seção transversal A = S da tabela
2. Área de Cortante: Esse parâmetro não é tão importante a menos que queira considerar as deformações causadas pelo esforço cortante. Portanto geralmente esse campo é deixado igual à área da seção transversal. Mas, caso queira calcular, basta somar todas as áreas dos elementos verticais, nesse caso, como o perfil está em pé foram somadas as áreas da alma e dos enrijecedores. Caso o perfil estivesse deitado somaríamos as áreas das abas apenas, pois quando o perfil está deitado a aba está na vertical
3. Momento de inércia I = Jx da tabela pois o perfil está em pé, se estivesse deitado adotaríamos Jy
4. Altura do perfil d = h da tabela pois o perfil está em pé, se estivesse deitado adotaríamos B
5. Distância da base do perfil até o CG – y = metade a altura do perfil pois está em pé, se estivesse deitado adotaríamos ey da tabela ou B-ey, sempre considerando que a cota deve ser tomada da parte inferior do perfil até o CG da peça.

Com esse recurso é possível então simular praticamente qualquer perfil, desde que se saiba as propriedades corretas. Caso você queira simular algum perfil e não encontra ele em nenhuma tabela de fabricante, ou resolveu inventar um perfil maluco, pode usar o recurso do Massprop do Autocad que eu ensino nesse vídeo aqui: https://www.youtube.com/watch?v=W7Mw6_Hq0VA

Atribuindo Carregamentos

Estamos quase concluindo a fase de modelagem (até que enfim…). Agora nos resta dizer para o programa quais são as cargas atuantes na estrutura. Para isso vamos iniciar criando carregamentos pontuais nos nós do banzo superior da nossa treliça:

Clique no ícone “Nodal Forces” no menu da barra superior do programa

Você já deve ter percebido que é sempre a mesma coisa, então devemos criar primeiro uma carga com um nome específico, selecionar os nós desejados segurando SHIFT e em seguida clicando sobre todos eles e depois de colocar os valores e direção da carga, devemos atribuir aos nós selecionados.

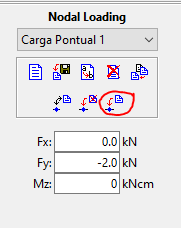
Depois de fazer isso a estrutura deve se parecer com isso:

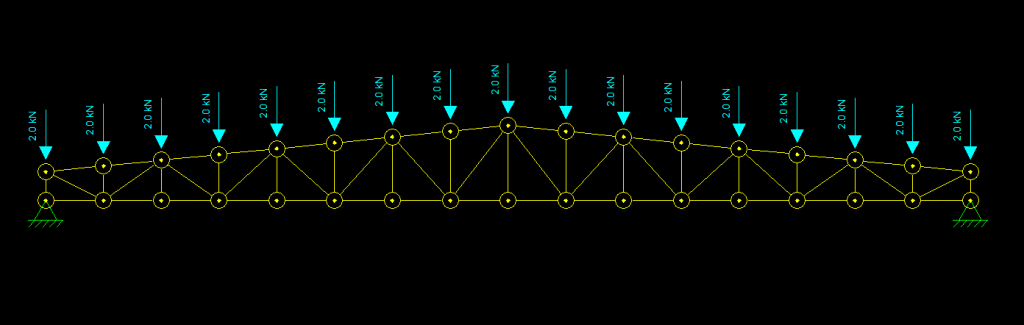
Veja que, para que as cargas apontassem para baixo, simulando o carregamento de Carga Permanente e Sobrecarga que as terças descarregam nos nós, foi necessário atribuir o valor -2,0 kN no eixo Y. O sinal negativo indica que a direção da carga aponta para o sentido negativo do eixo Y do modelo, portanto para baixo. Da mesma forma se atribuíssemos X positivo a carga apontaria para a direita, e se atribuíssemos X negativo a carga apontaria para a esquerda. Observe que nas cargas pontuais só é possível atribuir cargas nas direções X e Y do espaço de trabalho, ou em outras palavas, nas direções globais. Se você quiser uma carga inclinada, deve fazer o cálculo das componentes X e Y de acordo com o ângulo de inclinação e atribuir ao nó. Isso é ligeiramente diferente nas cargas distribuídas onde podemos gerar cargas perpendiculares ao eixo local das barras.

Para exemplificar esse outro tipo de carregamento, vamos atribuir um carregamento uniformemente distribuído no banzo superior, simulando uma carga de vento de 0,50 kN/m gerando sucção na cobertura. (Lembre-se que todos os valores aqui são fictícios e servem para ensinar a operar o programa, então não se preocupe se isso faz algum sentido em algum galpão real ou não)

Para isso primeiro vamos zerar os valores das cargas pontuais para não atrapalhar nossa visualização. Para isso basta selecionar as cargas pontuais e colocar o valor de Y igual a zero.

Agora clique no ícone “Uniform Loads”, crie uma carga denominada Vento Esquerdo, atribua ao eixo local Y o valor positivo de 0,50 kN/m e aplique ao banzo superior da água esquerda. Depois crie uma outra carga denominada Vento Direito e atribua ao eixo Local Y com o valor negativo, ou seja -0,50 kN/m. Isso deve ser feito pois quando criamos nosso modelo, utilizamos o recurso de espelhamento. Senão fizermos isso cada carga vai apontar em uma direção.

Após esse passo, o modelo deve ficar assim:

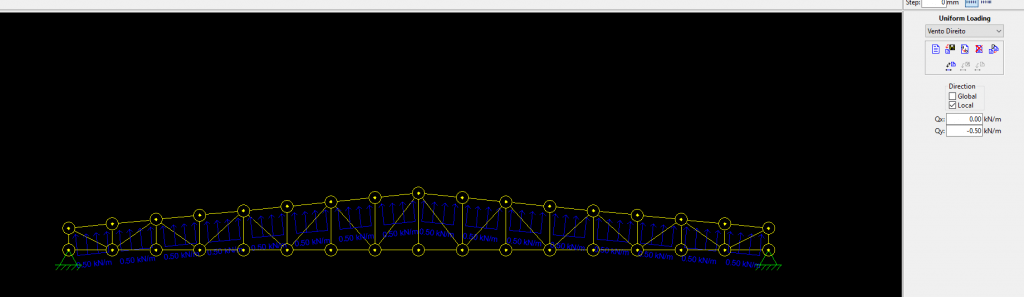
Observe que quando selecionamos eixos locais, as cargas ficam perpendiculares às barras do banzo superior. Caso você queira atribuir uma carga completamente vertical, atribua o parâmetro “Global”. Infelizmente não é possível que na mesma barra tenhamos cargas apontando para eixos globais e eixos locais, portanto uma prática muito comum em cálculo de coberturas e galpões é adotar os eixos globais no cálculo de vento, considerando as cargas totalmente verticais, como forma de aproximação.

Analisando a estrutura

Agora chega a parte mais legal de todas: fazer a análise da estrutura. Para isso vamos voltar ao modelo de treliça com cargas pontuais. Vou adotar cargas pontuais que fizemos anteriormente, mas antes é necessário fazer uma pequena adaptação. O ftool não calcula automaticamente o peso próprio da estrutura, portanto é necessário que isso seja feito manualmente e lançado como carga distribuída para refletir a realidade com maior fidelidade.

DICA: para saber o peso por metro linear de cada barra, basta multiplicar a área da seção transversal, em cm², da mesma por 0,7850, e multiplicar pela soma dos comprimentos (Length). Para saber a área da seção transversal de qualquer barra, basta clicar com o botão direito sobre ela e coletar as informações no painel direito:

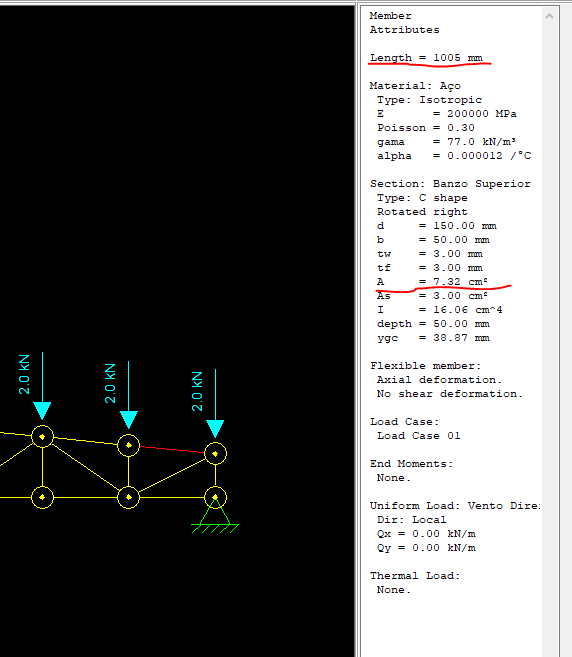
Peso Próprio de cada tipo de perfil:

U150 x 50 x 3 = 7,32 cm² x 0,7850 = 5,75 kg/m

2L38,1 x 3,2 = 4,67 cm² x 0,7850 = 3,66 kg/m

Peso próprio da treliça adotada:

Banzo Superior: Perfil U 150 x 50 x 3mm – 5,75 kg/m x 16,08m = 92,46 kg

Banzo Inferior: Perfil U 150 x 50 x 3mm – 5,75 kg/m x 16m = 92 kg

Diagonais e Montantes: 2L 38,1X3,2 – 3,66 kg/m x 36,63m = 134 kg

Peso Total da treliça: 92,46 + 92 + 134 = 318,52 kg

Peso médio linear da treliça: 318,52 / 16 = 19,90 kg/m

Observe que adotaremos o peso linear médio e distribuiremos sobre um dos banzos para simular o efeito do peso próprio. Geralmente eu adoto o banzo superior para considerar a hipótese mais severa. Isso é suficiente para uma análise satisfatória, mas caso deseje ser extremamente preciso, você pode aplicar o peso próprio de cada barra sobre ela mesma.

Vamos aplicar esse peso próprio sobre o banzo superior da treliça, sem esquecer de converter as unidades para kN/m:

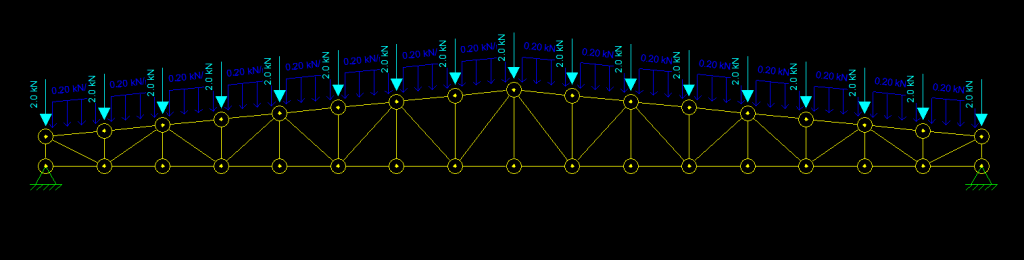
Agora vamos iniciar nossa análise.

Reações de apoio

Para que o programa exiba as reações de apoio e os resultados com as cargas, primeiro selecione o menu “Display> Reactions” e “Display> Reaction Values”. Marque também as opções destacadas.

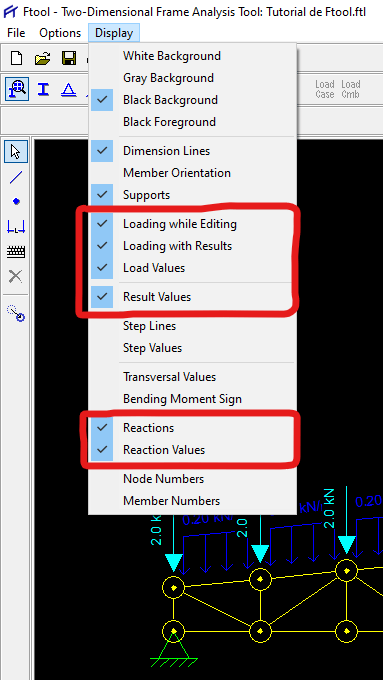
Analisando a curva deformada da estrutura (flecha)

Para verificar a curva deformada atuante na estrutura clique no ícone “Deformed Configuration” no canto superior direito do programa

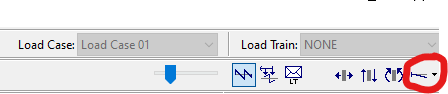
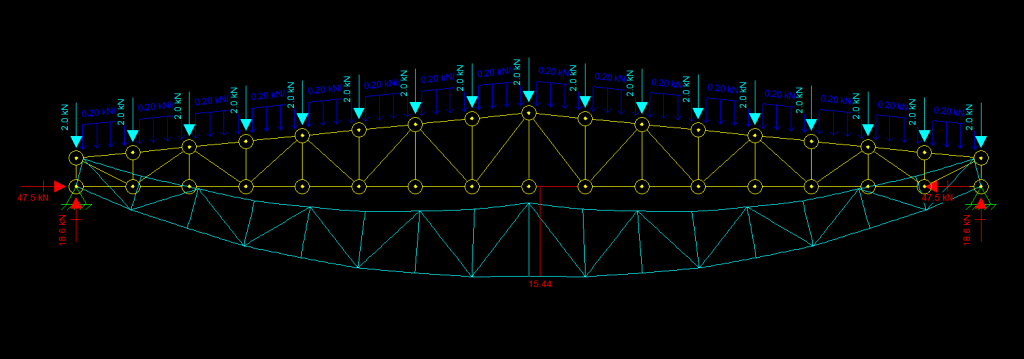
Você verá o formato da curva deformada da estrutura, e pode avaliar o valor de qualquer ponto clicando com o botão direito sobre a barra ou nó desejado. Esse valor será mostrado na tela do modelo e também na barra lateral direita do programa:

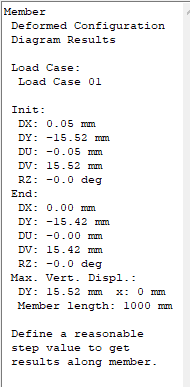
Ao clicar com o botão direito sobre o trecho da barra do banzo inferior à direita do montante central da treliça, obtemos o relatório acima. O campo INIT se refere aos valores de do nó inicial da barra enquanto o campo END se refere ao nó final da barra. Portanto nesse caso, o nó direito dessa barra se deslocou 0,05 mm para a direita (Sentido positivo do eixo X, campo DX), 15,52 mm para baixo (sentido negativo do eixo Y, DY). DU e DV se referem a coordenadas relativas dos mesmos deslocamentos. RZ indica que a rotação do nó direito não teve variação. O lado esquerdo do mesmo membro não teve deslocamento na direção X, deslocou-se 15,42 mm para baixo e também não apresentou rotação significativa. Isso pode ser observado também na tela se clicarmos próximo aos nós exibidos (É necessário aumentar o zoom ao máximo para não clicar sem querer no próprio nó):

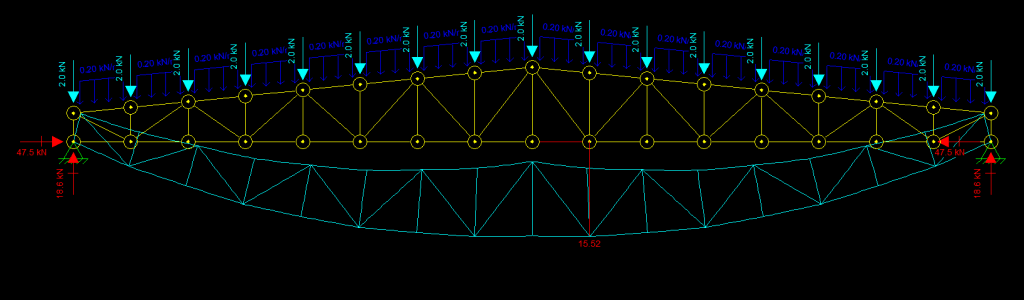
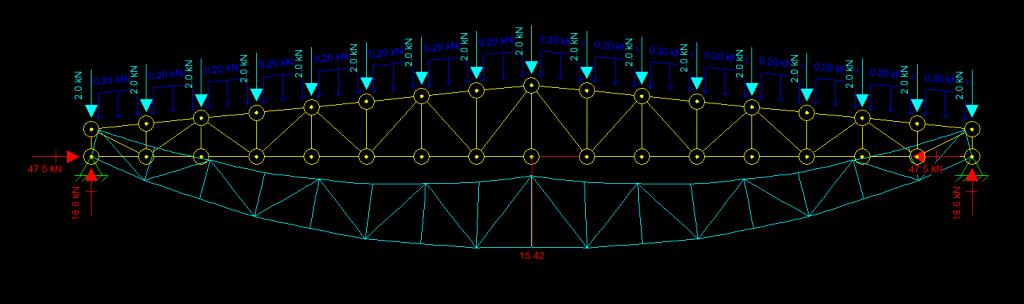
Agora basta ir alterando os perfis desejados ou até mesmo a geometria da treliça para adequar a estrutura à deformação máxima desejada pelo calculista. Lembre-se de que a cada vez que se altera os perfis, altera-se também o peso próprio da treliça. Como dica prática, mantenha o mesmo peso próprio aplicado até encontrar a deformação ideal, e depois atualize. Essa análise está diretamente ligada à avaliação da adequação da estrutura quanto aos Estados Limites de Serviço e deverá ser feita para cada hipótese de carregamento aplicável, por exemplo: Cargas Permanentes + Sobrecarga, Cargas Permanentes + Vento, Etc. Só prosseguimos com as verificações de Estados Limites Últimos quando a estrutura estiver dentro dos limites previstos pela Tabela C.1 da NBR8800, ou dentro de padrões aceitáveis em literaturas de Estados Limites de Serviço mais específicas.

Extraindo esforços atuantes

Após efetuar a análise dos Estados Limites de Serviço, é necessário verificar se as peças suportam individualmente os esforços atuantes sem sofrer nenhum efeito relacionado aos Estados Limites Últimos (Escoamento, Flambagem, Instabilidade, Ruptura, etc…). Para isso é necessário lançar as cargas com as devidas majorações previstas pela tabela 1 da NBR8800. Volto a lembrar, se você não tem ideia do que está acontecendo aqui, por favor veja essas aulas gratuitas do primeiro módulo do curso de projeto e cálculo de estruturas metálicas online.

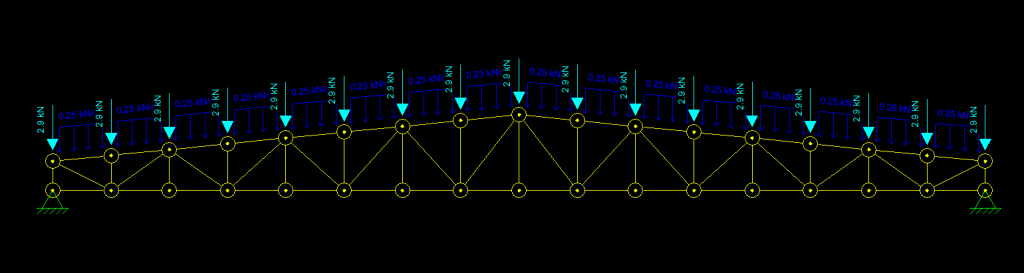
Como estamos avaliando uma estrutura de treliça plana, nos interessa somente os valores de Tração e Compressão obtidos. Para isso clique no ícone “Axial Force” na canto superior direito da tela. Aproveite e ajuste a escala com o ícone deslizante ao lado:

Quando isso for feito, você verá em cada barra os valores de tração (positivos) e compressão (negativos).

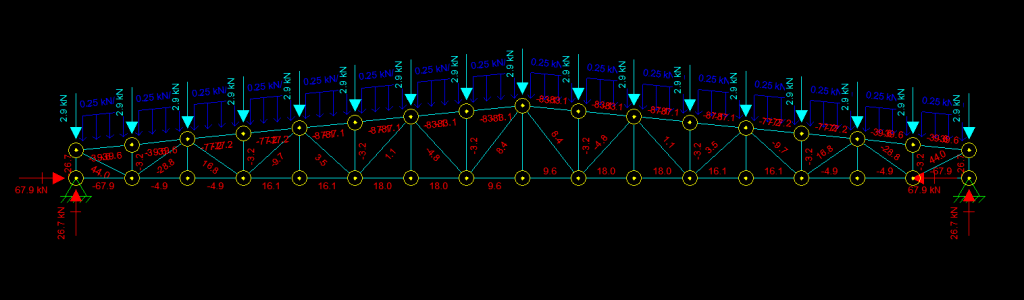
Com esses valores basta seguir o roteiro de verificação dos estados limites últimos para cada barra, para cada carregamento e combinação de cargas.

As reações de apoio apresentadas serão utilizadas para dimensionar os chumbadores e consoles a serem dimensionados para suportar a estrutura, bem como podem ser passadas para o calculista do concreto armado para que o mesmo dimensione os pilares para suportar essas cargas.

Elaborando a análise com pilares de aço.

Vamos sentir o efeito da colocação de pilares no nosso modelo. Para isso vou introduzir duas barras de 6000 mm em cada extremidade e selecionar para elas um perfil laminado I de abas paralelas W310X21, com base teoricamente engastada. Para isso primeiro remova as vinculações externas dos nós de apoio da treliça, selecionando-os e atribuindo a eles a vinculação “free” em todos os graus de liberdade. Depois modele o pilar atribuindo a eles a vinculação externa “Fix” em todos os graus de liberdade. Não esqueça de atribuir o material “Aço” a eles, e também crie um rótulo de perfil chamado “Pilar”, com a biblioteca de perfis Gerdau Açominas e selecione o perfil W310X21:

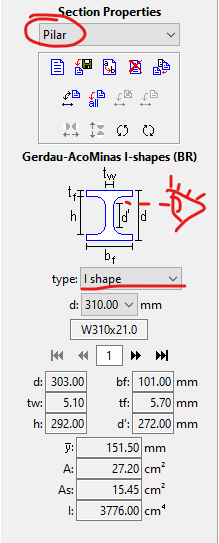
Tenha sempre atenção quanto à posição do perfil, pois nesse caso queremos que a maior inércia do perfil esteja no plano da treliça para que a deformação seja a menor possível. Ou seja, quem olhar o pórtico de frente vai automaticamente ver a alma do pilar, portanto o nosso “observador imáginário” deve ver a mesma coisa na hora de selecionar o perfil do ftool. Após atribuir os parâmetros ao pilar nossa análise de deformação deve se parecer com isso (Não se esqueça de retornar às cargas de verificação de ELS, ou seja, sem majoração).

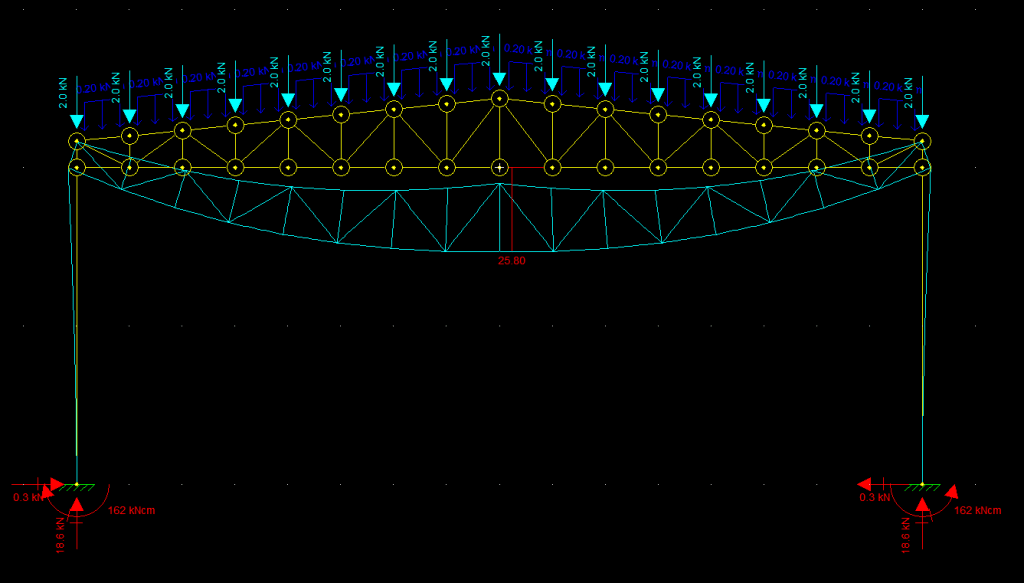
Observe que o deslocamento máximo da mesma barra que analisamos anteriormente aumentou cerca de 10mm. Isso acontece pois, como você pode observar, há também um deslocamento horizontal do pilar, que se reflete no deslocamento vertical no centro da treliça. Agora nossa análise está sujeita a uma série de variáveis que podemos explorar para alterar o comportamento final da estrutura. Podemos alterar a vinculação. Vamos atribuir ao pilar ligações rígidas entre si, ou seja, remover as articulações somente do pilar considerar que a treliça não é somente apoiada sobre a cabeça do pilar, mas sim fixada com seus dois banzos chegando na mesa do pilar.

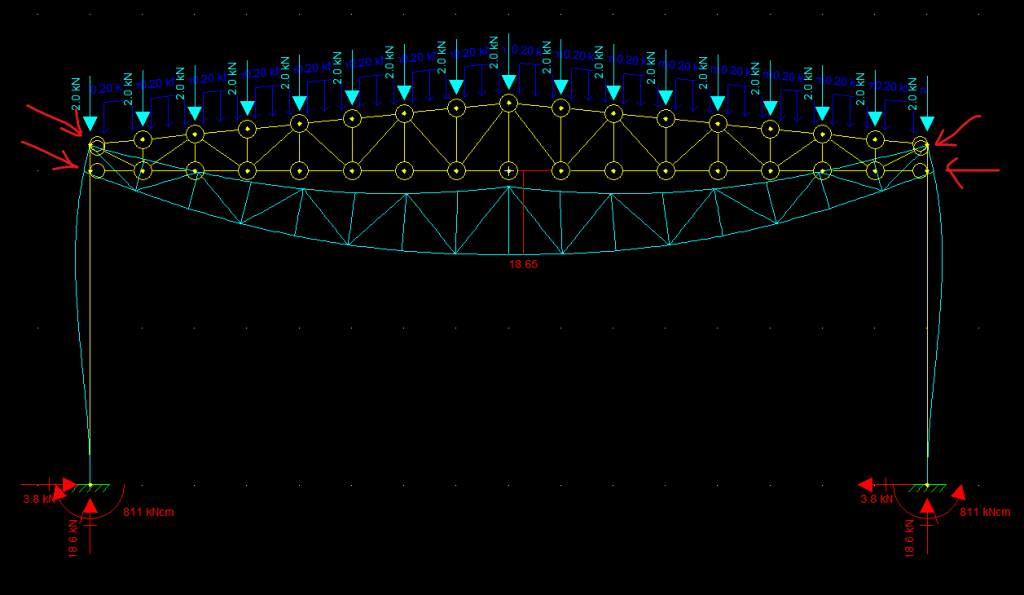
Veja que todos os nós da barra do pilar são considerados rígidos, e apenas os nós da treliça são articulados. Veja também que estendemos o pilar até o topo da treliça, fazendo assim com que o banzo superior também esteja vinculado ao pilar rígido, oferecendo assim uma maior rigidez ao sistema. Agora podemos brincar com outra variável, vamos alterar a inércia do pilar. Podemos trocar para um pilar de maior inércia como um W530X66 por exemplo e ver o que acontece:

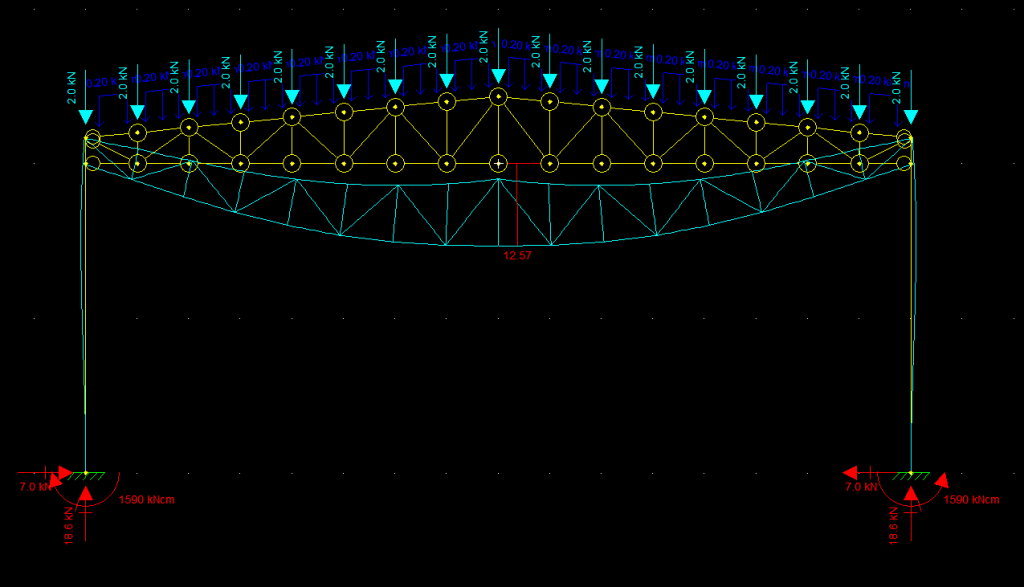
Observe que a flecha cai de 18,65 mm para 12,57mm, mas também as reações de apoio horizontal e momentos fletores são acentuadas. Isso corre pois se trata de um sistema hiperestático que depende da rigidez das peças para se calcular a correta deformação e reações. Podemos aliviar esse efeito alterando a vinculação externa do pilar para apoios de segundo gênero e ver o efeito disso:

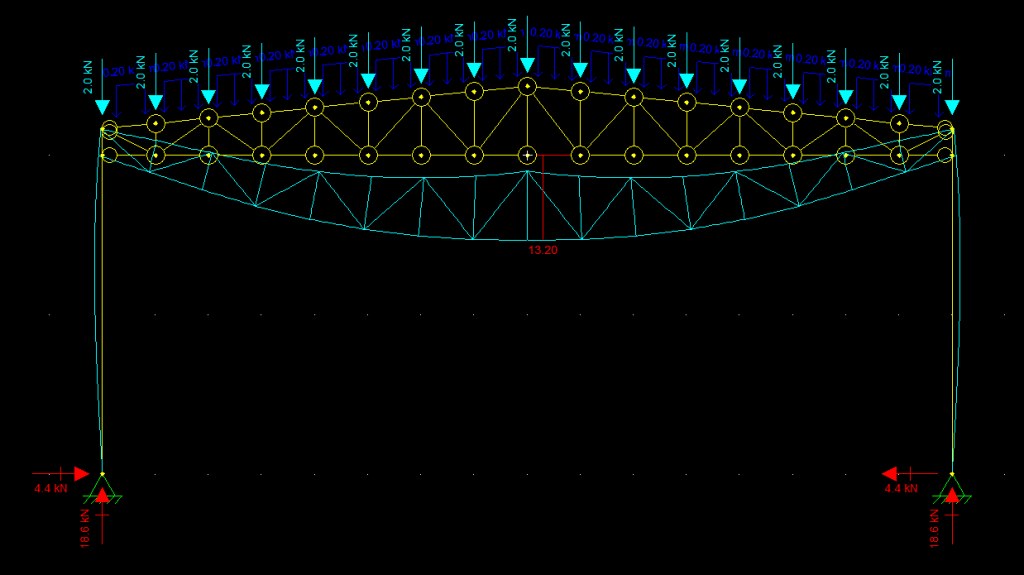
Aliviamos as bases e aumentamos um pouco as flechas. E assim vamos fazendo até chegar ao valor que desejamos. Vamos manter essa geometria e alterar o pilar para um 310X23,8 e voltar com as cargas majoradas para analisar os esforços atuantes:

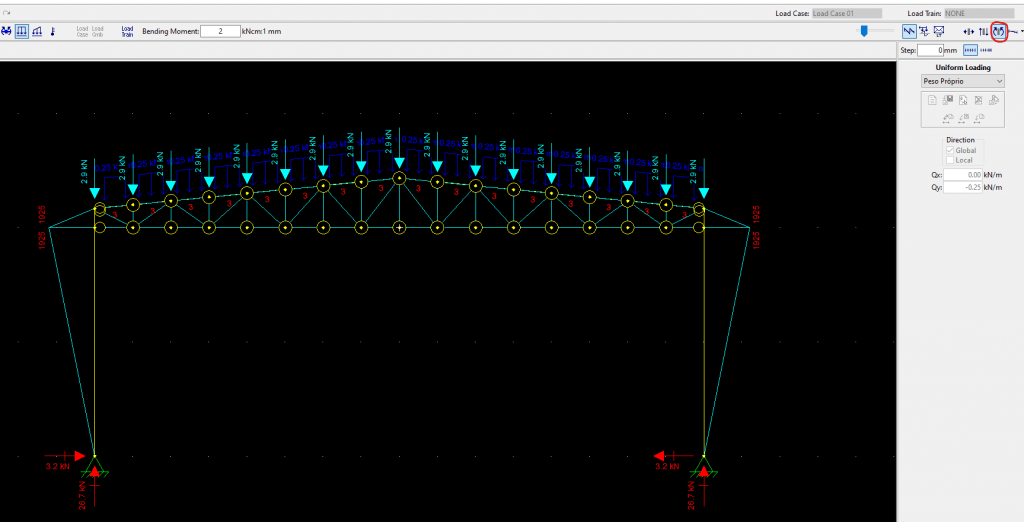
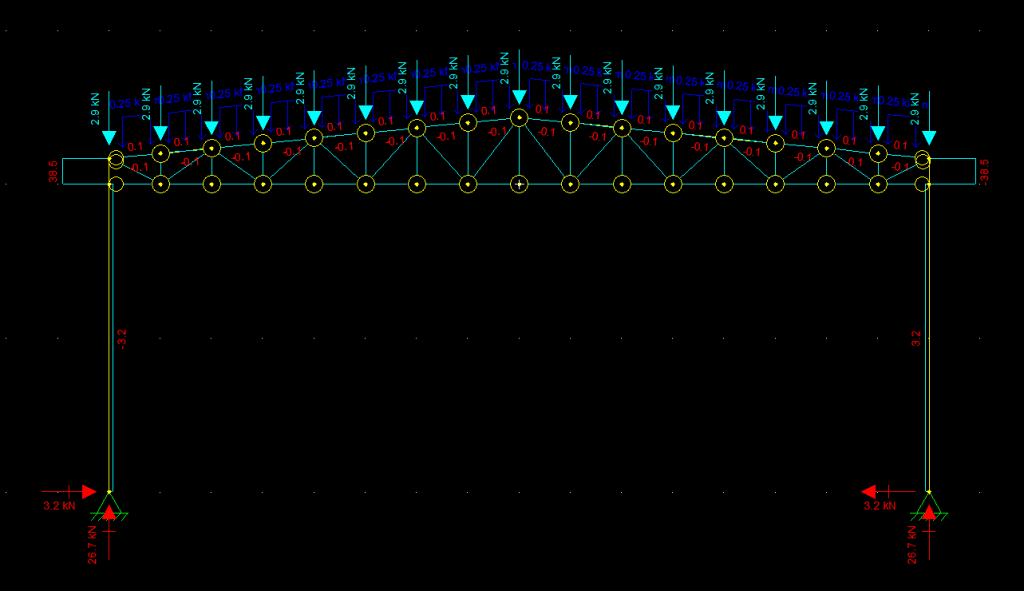
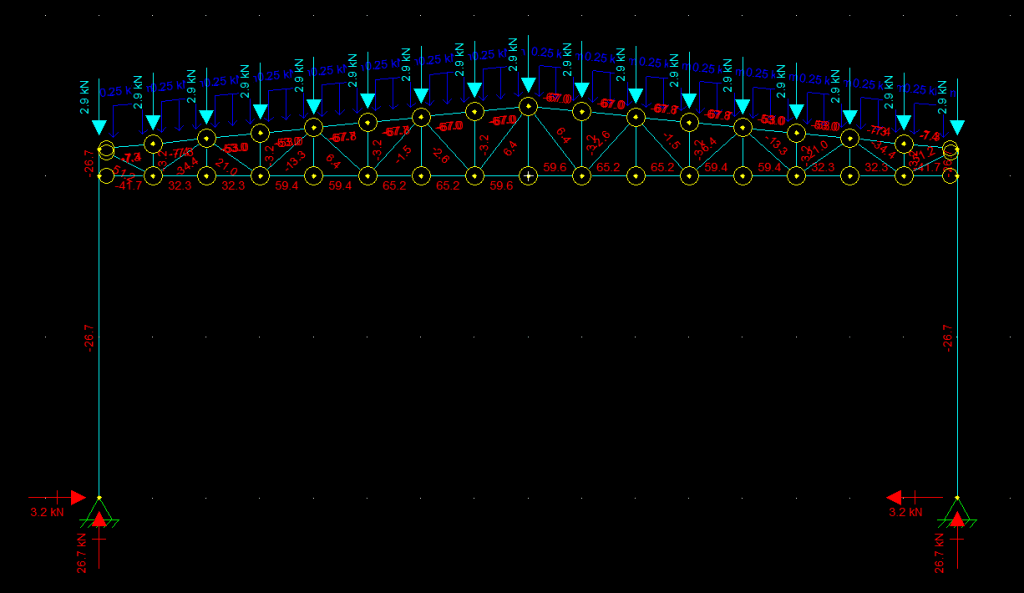
Observe os valores obtidos nesse modelo e compare com o modelo simplesmente apoiado que fizemos inicialmente. Muita diferença, não é? E esses valores vão variar conforme mudamos as condições de apoio, inércia do pilar, vinculação entre as barras, inércia das barras, etc. Portanto, sabendo disso você mesmo pode responder quando te perguntarem: “Posso colocar somente o apoio e depois aplicar a reação sobre o pilar?”. A resposta é simples: Depende, mas o ideal é não.

E se o pilar for de concreto?

Ok mas e se o pilar for de concreto, faz alguma diferença? Vamos ver.

A primeira coisa que devemos fazer é definir um material para chcmar de concreto. Veja que o Ftool nos pede o módulo de elasticidade. Vamos ver o que a NBR6118 nos diz a respeito disso:

Em outras palavras, o módulo de elasticidade a ser considerado deve ser Ecs = 0,85 . 5600 fck^ (0,5). Considerando um fck conservador de 20MPa, temos Ecs = 0,85 . 5600 . 20^(0,5) = 21287 MPa. Se você conhecer o fck final da estrutura, fique à vontade para introduzir esse valor nos parâmetros.

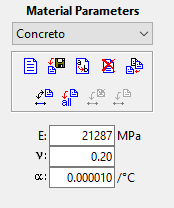
Agora basta criar a seção transversal desejada. No exemplo vamos adotar Seção Retangular 20X40:

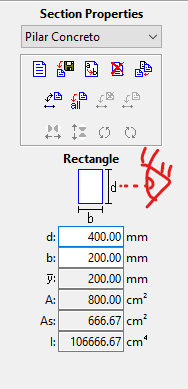
Agora vamos atribuir isso ao nosso modelo, considerando as bases engastadas.

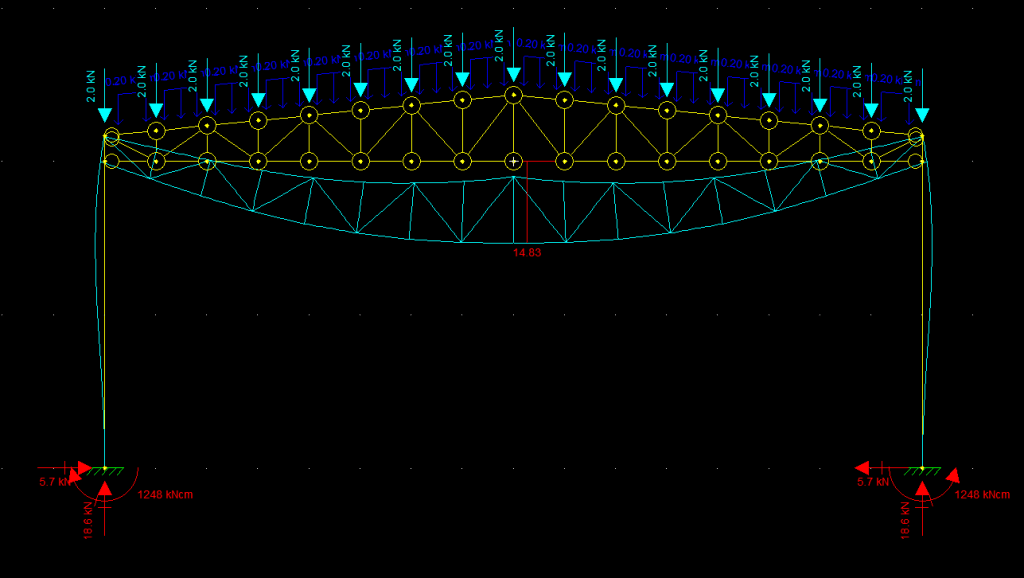
E assim podemos simular um pilar de concreto que recebe uma estrutura metálica de cobertura.

Se você acompanhou esse tutorial do começo ao fim, repetindo os exemplos que adotamos durante o processo, você será capaz de modelar corretamente qualquer estrutura, seja de pórticos rígidos, vigas simples, ou sistemas treliçados. Agora, fazer a análise conforme as normas são outros quinhentos, é necessário estudar muito mais. Se você quer realmente se aprofundar e dominar o cálculo de estruturas metálicas com segurança, e ser um profissional completo, não deixe de conhecer o curso que eu desenvolvi clicando aqui. É o único curso que vai te oferecer uma formação completa, capacitando-o a calcular manualmente, e com softwares, com suporte a dúvidas, acesso vitalício e exemplos sempre atualizados. Clique aqui para saber mais.

Grande abraço a todos e até a próxima

Eng. Felipe Jacob